计算机图形学实验一 基本图形的生成算法

050

一、实验目的

1、进一步熟悉CDC图形程序库；

2、掌握直线的中点Bresenham生成算法、数值微分直线生成算法；

3、掌握圆的中点Bresenham生成算法；

4、掌握椭圆的中点Bresenham生成算法。

二、实验性质

验证性

三、实验要求

1、认真阅读本次实验的目的，清楚本次实验要求和实验内容；

2、能够根据实验指导书的要求，独立完成相关的内容；

3、根据直线的中点Bresenham生成算法和数值微分生成算法，完成任意直线的绘制。

4、根据圆的中点Bresenham生成算法思想和圆的对称性，完成圆的绘制；

5、根据椭圆的中点Bresenham生成算法思想和椭圆的对称性， 完成椭圆的绘制。

四、实验内容

1、根据中点Bresenham直线生成算法思想，完成任意斜率直线的绘制。

(1) 创建一个新的MFC项目，如下图所示。

 

 

(2) 在view.h头文件中添加起点p0和终点p1，以及基于中点Bresenham的直线绘制函数void DrawLine_MB(CDC *pDC, CPoint p0, CPoint p1);

        protected:

           CPoint p0; // 定义直线的起点

           CPoint p1; // 定义直线的终点

           void DrawLine_MB(CDC *pDC, CPoint p0, CPoint p1);

                 //void DrawLine_DDA(CDC *pDC, CPoint p0, CPoint p1);

(3) 在菜单“项目”中点击“类向导”，如下图所示。

 (4) 在弹出的“MFC类向导”对话框中，在“类名”中选择“CView”类，在“消息”选项卡中选择“WM_LBUTTONDOWN”，然后点击“添加处理程序(A)…”，如下图所示。

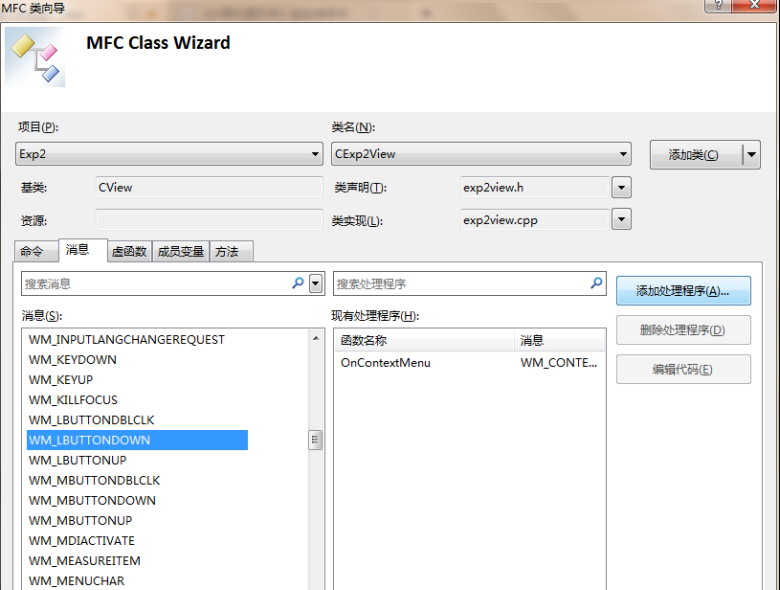
(5) 类似地，在“MFC类向导”对话框中，在“类名”中选择“CView”类，在“消息”选项卡中选择“WM_LBUTTONUP”，然后点击“添加处理程序(A)…”。

(6) 在CView.cpp文件中void CExp2View::OnLButtonDown(UINT nFlags, CPoint point)函数添加代码，获得直线的起点坐标。

  void CExp2View::OnLButtonDown(UINT nFlags, CPoint point)

{

// TODO: 在此添加消息处理程序代码和/或调用默认值

CRect rect; //定义矩形

GetClientRect(&rect); //获得客户区矩形的大小

p0.x=point.x; //将当前鼠标按下的点作为起点坐标

p0.y=point.y;

p0.x=p0.x-rect.Width()/2;  //设备坐标系向自定义坐标系转换

p0.y=rect.Height()/2-p0.y;

CView::OnLButtonDown(nFlags, point);

}

 (7)  在CView.cpp文件中void CExp2View::OnLButtonUP(UINT nFlags, CPoint point)函数添加代码，获得直线的终点坐标，并绘制直线。

 void CExp2View::OnLButtonUp(UINT nFlags, CPoint point)
{
	// TODO: 在此添加消息处理程序代码和/或调用默认值
	p1.x=point.x; //将当前释放鼠标的点作为终点
	p1.y=point.y;

	CRect rect; //定义矩形 
	GetClientRect(&rect); //获得客户区矩形的大小
	
	CDC *pDC=GetDC();                                   //定义设备上下文指针
	pDC->SetMapMode(MM_ANISOTROPIC);                    //自定义坐标系
	pDC->SetWindowExt(rect.Width(),rect.Height());      //设置窗口比例
	pDC->SetViewportExt(rect.Width(),-rect.Height()); //设置视区x轴水平向右，y轴垂直向上
	pDC->SetViewportOrg(rect.Width()/2,rect.Height()/2); //设置客户区中心为坐标系原点
		
	p1.x=p1.x-rect.Width()/2;    //原始设备坐标系向自定义坐标系转换
	p1.y=rect.Height()/2-p1.y;
	
	DrawLine_MB(pDC, p0, p1); //采用中点Bresenham直线生成算法绘制直线
	ReleaseDC(pDC);
	CView::OnLButtonUp(nFlags, point);
}

(8) 在CView.cpp文件中void CExp2View::DrawLine_MB(CDC *pDC, CPoint p0, CPoint p1)函数中添加代码，实现中点Bresenham直线生成算法。

void Ctest1View::DrawLine_MB(CDC* pDC, CPoint p0, CPoint p1)
{
	CPoint t, p;
	int dx = p1.x - p0.x;
	int dy = p1.y - p0.y;
	double dc = 1 / (double)dx;
	if (abs(p0.x - p1.x) == 0)//绘制垂直线
	{
		if (p0.y > p1.y)  //交换顶点,使得起始点低于终点
		{
			t = p0; p0 = p1; p1 = t;
		}
		for (p = p0; p.y < p1.y; p.y++)
		{
			double r, g, b;
			r = (1 - (p.y - p0.y)), g = 0, b = (p.y - p0.y);
			pDC->SetPixelV(p, RGB(r * 255, g * 255, b * 255));
			//pDC->SetPixelV(p.x, p.y, RGB(0, 0, 0));
		}
	}
	else
	{
		double k, d;
		k = double(p1.y - p0.y) / double(p1.x - p0.x);
		if (0.0 <= k && k <= 1.0) //绘制0<=k<=1 的直线
		{
			if (p0.x > p1.x) //交换顶点
			{
				t = p0; p0 = p1; p1 = t;
			}
			d = 0.5 - k; //初始中点误差值

			for (p = p0; p.x < p1.x; p.x++)
			{
				//请在这里添加代码，描绘直线上的像素点
				double r, g, b;
				r = (1 - (p.x - p0.x) * dc), g = 0, b = (p.x - p0.x) * dc;
				pDC->SetPixelV(p, RGB(r * 255, g * 255, b * 255));
				//pDC->SetPixelV(p.x, p.y, RGB(0, 0, 0));

				if (d < 0) {
					p.y++;
					d++;
				}
				else {
					d = d - k;
				}
			}
		}

		else if (k > 1.0) //绘制k>1 的直线
		{
			if (p0.y > p1.y) //交换顶点
			{
				t = p0; p0 = p1; p1 = t;
			}
			d = 1 - 0.5 * k;  //初始中点误差值
			for (p = p0; p.y < p1.y; p.y++)
			{
				//请在这里添加代码，描绘直线上的像素点
				double r, g, b;
				r = (1 - (p.x - p0.x) * dc), g = 0, b = (p.x - p0.x) * dc;
				pDC->SetPixelV(p, RGB(r * 255, g * 255, b * 255));
				//pDC->SetPixelV(p.x, p.y, RGB(0, 0, 0));
				if (d < 0) {
					d = d + 1;
				}
				else {
					p.x++;
					d = d + 1 - k;
				}
			}
		}

		else if (k >= -1.0 && k < 0.0)//绘制-1<=k<0的直线
		{
			if (p0.x > p1.x)  //交换顶点
			{
				t = p0; p0 = p1; p1 = t;
			}
			d = -0.5 - k;
			for (p = p0; p.x < p1.x; p.x++)
			{       //描绘直线上的像素点
				double r, g, b;
				r = (1 - (p.x - p0.x) * dc), g = 0, b = (p.x - p0.x) * dc;
				pDC->SetPixelV(p, RGB(r * 255, g * 255, b * 255));
				//pDC->SetPixelV(p.x, p.y, RGB(0, 0, 0));
				if (d > 0)
				{
					p.y--;
					d -= 1 + k;
				}
				else
					d -= k;
			}
		}
		else if (k < -1.0)//绘制k<-1的直线 
		{
			if (p0.y < p1.y) //交换顶点
			{
				t = p0; p0 = p1; p1 = t;
			}
			d = -1 - 0.5 * k;
			for (p = p0; p.y > p1.y; p.y--)
			{       //描绘直线上的像素点
				double r, g, b;
				r = (1 - (p.x - p0.x) * dc), g = 0, b = (p.x - p0.x) * dc;
				pDC->SetPixelV(p, RGB(r * 255, g * 255, b * 255));
				//pDC->SetPixelV(p.x, p.y, RGB(0, 0, 0));
				if (d < 0)
				{
					p.x++;
					d -= 1 + k;
				}
				else
					d -= 1;
			}
		}
	}
	p0 = p1;
}

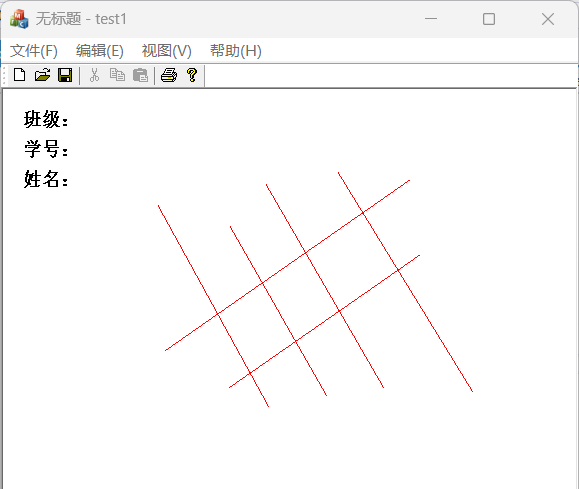
（9）运行该项目，并可通过先按下鼠标左键、再释放鼠标左键，绘制任意斜率的直线，如下图所示。

实际运行结果：

2、根据数值微分直线生成算法思想， 完成如上图所示的任意斜率直线的绘制。

（1）类似以上步骤，在view.h头文件中添加基于数值微分DDA的直线绘制函数DrawLine_DDA();

（2）在CView.cpp文件中void CExp2View::DrawLine_DDA(CDC *pDC, CPoint p0, CPoint p1)函数中添加代码，实现数值微分DDA直线生成算法。

 void Ctest1View::DrawLine_DDA(CDC* pDC, CPoint p0, CPoint p1)
{
	CPoint t, p;
	if (abs(p0.x - p1.x) == 0)//绘制垂直线
	{
		if (p0.y > p1.y)  //交换顶点,使得起始点低于终点
		{
			t = p0; p0 = p1; p1 = t;
		}
		for (p = p0; p.y < p1.y; p.y++)
		{
			pDC->SetPixelV(p.x, p.y, RGB(255, 0, 0));
		}
	}
	else
	{
		double k;
		k = double(p1.y - p0.y) / double(p1.x - p0.x);
		if ((0.0 <= k && k <= 1.0) || (k >= -1.0 && k < 0.0)) //绘制0<=k<=1 或-1<=k<0的直线
		{
			if (p0.x > p1.x) //交换端点
			{
				t = p0; p0 = p1; p1 = t;
			}

			double y = p0.y;
			for (p = p0; p.x < p1.x; p.x++) //以x为主方向进行移动
			{
				//请在这里添加代码，描绘直线上的像素点
				pDC->SetPixelV(p.x, p.y, RGB(255, 0, 0));
				y = y + k;
				if (y >= 0) {
					p.y = int(y + 0.5);
				}
				else {
					p.y = int(y - 0.5);
				}

			}
		}


		else if ((k > 1.0) || k < -1.0)//绘制k>1或k<-1的直线
		{
			if (p0.y > p1.y) //交换端点
			{
				t = p0; p0 = p1; p1 = t;
			}

			double x = p0.x;
			for (p = p0; p.y < p1.y; p.y++) //以y为主方向进行移动
			{
				//请在这里添加代码，描绘直线上的像素点
				pDC->SetPixelV(p.x, p.y, RGB(255, 0, 0));
				x = x + 1 / k;
				if (x >= 0) {
					p.x = int(x + 0.5);
				}
				else {
					p.x = int(x - 0.5);
				}
			}
		}
	}
}

 

（3）在CView.cpp文件中void CExp2View::OnLButtonUP(UINT nFlags, CPoint point)函数中调用DrawLine_DDA，即利用DDA生成直线算法绘制直线。

 

void Ctest1View::DrawLine_DDA(CDC* pDC, CPoint p0, CPoint p1)
{
	CPoint t, p;

	if (abs(p0.x - p1.x) == 0) // 绘制垂直线
	{
		if (p0.y > p1.y)  // 交换顶点,使得起始点低于终点
		{
			t = p0; p0 = p1; p1 = t;
		}
		for (p = p0; p.y < p1.y; p.y++)
		{
			pDC->SetPixelV(p.x, p.y, RGB(255, 0, 0));
		}
	}
	else
	{
		double k;
		k = double(p1.y - p0.y) / double(p1.x - p0.x);

		if ((0.0 <= k && k <= 1.0) || (k >= -1.0 && k < 0.0)) // 绘制0<=k<=1 或-1<=k<0的直线
		{
			if (p0.x > p1.x) // 交换端点
			{
				t = p0; p0 = p1; p1 = t;
			}

			double y = p0.y;
			for (p = p0; p.x < p1.x; p.x++) // 以x为主方向进行移动
			{
				pDC->SetPixelV(p.x, round(y), RGB(255, 0, 0));
				y = y + k;
			}
		}
		else if ((k > 1.0) || k < -1.0) // 绘制k>1或k<-1的直线
		{
			if (p0.y > p1.y) // 交换端点
			{
				t = p0; p0 = p1; p1 = t;
			}

			double x = p0.x;
			for (p = p0; p.y < p1.y; p.y++) // 以y为主方向进行移动
			{
				pDC->SetPixelV(round(x), p.y, RGB(255, 0, 0));
				x = x + 1.0 / k;
			}
		}
	}

}

 

3、根据圆的中点Bresenham生成算法思想和圆的对称性，完成圆的绘制。

(1) 创建一个新的MFC项目，如下图所示。

(2) 在view.h头文件中添加圆的某条直径的起点p0和终点p1，以及基于中点Bresenham的圆绘制函数void DrawCircle_MB(CDC *pDC, CPoint p0, CPoint p1);

 protected:

           CPoint p0; // 定义直径的起点

           CPoint p1; // 定义直径的终点

           void DrawCircle_MB(CDC *pDC, CPoint p0, CPoint p1);

 (3) 在菜单“项目”中点击“类向导”，如下图所示。

(4) 在弹出的“MFC类向导”对话框中，在“类名”中选择“CView”类，在“消息”选项卡中选择“WM_LBUTTONDOWN”，然后点击“添加处理程序(A)…”，如下图所示。

(5) 类似地，在“MFC类向导”对话框中，在“类名”中选择“CView”类，在“消息”选项卡中选择“WM_LBUTTONUP”，然后点击“添加处理程序(A)…”。

(6) 在CView.cpp文件中void CExp3View::OnLButtonDown(UINT nFlags, CPoint point)函数添加代码，获得直径的起点坐标。

 

  void CExp3View::OnLButtonDown(UINT nFlags, CPoint point)
{
	// TODO: 在此添加消息处理程序代码和/或调用默认值
	CRect rect; //定义矩形 
	GetClientRect(&rect); //获得客户区矩形的大小

	p0.x=point.x; //将当前鼠标按下的点作为起点坐标
	p0.y=point.y;
	p0.x=p0.x-rect.Width()/2;  //设备坐标系向自定义坐标系转换
	p0.y=rect.Height()/2-p0.y;
	CView::OnLButtonDown(nFlags, point);
}

(7) 在CView.cpp文件中void CExp3View::OnLButtonUP(UINT nFlags, CPoint point)函数添加代码，获得直径的终点坐标，并绘制圆。

 void CExp3View::OnLButtonUp(UINT nFlags, CPoint point)
{
	// TODO: 在此添加消息处理程序代码和/或调用默认值
	p1.x=point.x; //将当前释放鼠标的点作为终点
	p1.y=point.y;

	CRect rect; //定义矩形 
	GetClientRect(&rect); //获得客户区矩形的大小
	
	CDC *pDC=GetDC();                                   //定义设备上下文指针
	pDC->SetMapMode(MM_ANISOTROPIC);                    //自定义坐标系
	pDC->SetWindowExt(rect.Width(),rect.Height());      //设置窗口比例
	pDC->SetViewportExt(rect.Width(),-rect.Height()); //设置视区x轴水平向右，y轴垂直向上
	pDC->SetViewportOrg(rect.Width()/2,rect.Height()/2); //设置客户区中心为坐标系原点
		
	p1.x=p1.x-rect.Width()/2;    //原始设备坐标系向自定义坐标系转换
	p1.y=rect.Height()/2-p1.y;
	
	DrawCircle_MB(pDC, p0, p1);  //采用中点Bresenham直线生成算法绘制圆
	ReleaseDC(pDC);
	CView::OnLButtonUp(nFlags, point);

}

(8) 在CView.cpp文件中void CExp3View::DrawCircle_MB(CDC *pDC, CPoint p0, CPoint  p1)函数中添加代码，实现圆的中点Bresenham生成算法。

void Ctest2View::DrawCircle_MB(CDC *pDC, CPoint p0, CPoint p1)  //绘制圆的函数
{
	CPoint center; //圆心
	center.x = (p0.x + p1.x) / 2.0; center.y = (p0.y + p1.y) / 2.0; //计算圆心坐标
	double r = sqrt(1.0*(p1.x - p0.x)*(p1.x - p0.x) + 1.0*(p1.y - p0.y)*(p1.y - p0.y)) / 2.0;//计算圆的半径     

	int x, y;
	double d;
	d = 1.25 - r;
	x = 0;
	y = (int)r;

	while (x <= y)
	{
		// 绘制八分圆上的点
		pDC->SetPixel(center.x + x, center.y + y, RGB(0, 0, 0));
		pDC->SetPixel(center.x - x, center.y + y, RGB(0, 0, 0));
		pDC->SetPixel(center.x + x, center.y - y, RGB(0, 0, 0));
		pDC->SetPixel(center.x - x, center.y - y, RGB(0, 0, 0));
		pDC->SetPixel(center.x + y, center.y + x, RGB(0, 0, 0));
		pDC->SetPixel(center.x - y, center.y + x, RGB(0, 0, 0));
		pDC->SetPixel(center.x + y, center.y - x, RGB(0, 0, 0));
		pDC->SetPixel(center.x - y, center.y - x, RGB(0, 0, 0));

		if (d < 0)
		{
			d += 2 * x + 3;
		}
		else
		{
			d += 2 * (x - y) + 5;
			y--;
		}
		x++;
	}
}

(9) 运行该项目，并可通过先按下鼠标左键、再释放鼠标左键，绘制任意大小的圆，如下图所示。

运行结果如图所示：

 

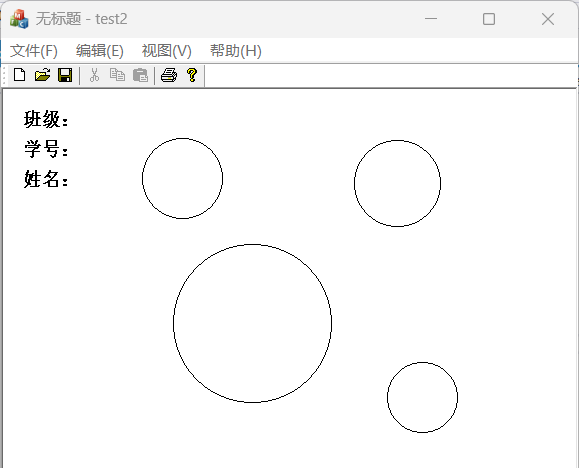
4、根据椭圆的中点Bresenham生成算法思想和椭圆的对称性，完成椭圆的绘制。

(1) 类似以上步骤，在view.h头文件中添加基于中点Bresenham的椭圆绘制函数void DrawEllipse_MB(CDC *pDC, CPoint p0, CPoint p1);以及绘画对称点函数 void EllipsePoint(int x, int y, CDC *pDC)

 (2) 在CView.cpp文件中void CExp3View::EllipsePoint(int x, int y,CDC *pDC)函数中添加代码，根据点(x, y)描绘其他象限的对称点。

 void Ctest2View::EllipsePoint(int x, int y,CDC *pDC) //四分法画椭圆子函数
{
	CPoint center; //椭圆中心
	center.x=(p0.x+p1.x)/2.0; center.y=(p0.y+p1.y)/2.0; //计算椭圆中心坐标

	COLORREF  clr=RGB(0,0,255);                         //定义椭圆颜色
	pDC->SetPixelV(x+center.x,y+center.y,clr);
	pDC->SetPixelV(-x+center.x,y+center.y,clr);
	pDC->SetPixelV(x+center.x,-y+center.y,clr);
	pDC->SetPixelV(-x+center.x,-y+center.y,clr);	
  }

(3) 在CView.cpp文件中void CExp3View::DrawEllipse_MB(CDC *pDC, CPoint p0, CPoint p1)函数中添加代码，实现椭圆的中点Bresenham生成算法。

 void Ctest2View::DrawEllipse_MB(CDC *pDC, CPoint p0, CPoint p1) //绘制圆的函数
{
	double a, b, d1, d2;
	a = abs(p1.x - p0.x) / 2.0; //椭圆半轴
	b = abs(p1.y - p0.y) / 2.0; //椭圆半轴
	int x, y;
	x = 0; y = b;
	d1 = b * b + a * a * (-b + 0.25);         //椭圆AC弧段的中点误差项初始值
	EllipsePoint(x, y, pDC);
	while (b * b * (x + 1) < a * a * (y - 0.5))  //椭圆AC弧段
	{ //请在以下位置添加代码绘制椭圆AC弧段

		if (d1 < 0) {
			d1 += b * b * (2 * x + 3);
		}
		else
		{
			d1 += b * b * (x * 2 + 3) + a * a * (-2 * y + 2);
			y--;
		}
		x++;
		EllipsePoint(x, y, pDC);

	}
	d2 = b * b * (x + 0.5) * (x + 0.5) + a * a * (y - 1) * (y - 1) - a * a * b * b;//椭圆CB弧段的中点误差项初始值
	while (y > 0) //椭圆CB弧段
	{

		if (d2 < 0)
		{
			d2 += b * b * (2 * x + 2) + a * a * (-2 * y + 3);
			x++;
		}
		else
		{
			d2 += a * a * (-2 * y + 3);
		}
		y--;
		EllipsePoint(x, y, pDC);
	}
}

 

（4）在CView.cpp文件中void CExp3View::OnLButtonUP(UINT nFlags, CPoint point)函数中调用DrawEllipse_MB( )，即利用中点Bresenham生成算法绘制椭圆，效果如下图所示。

运行结果如图所示：

 

 

五、思考题

1、请问按下鼠标左键或释放鼠标左键时，所获得鼠标当前所指向的点坐标是以哪个坐标系为参考？

自己写

2、如何生成反走样（即抗锯齿）的直线？ 请尝试编写代码。

自己写

3、假设两端点颜色分别为绿色和红色，如何生成颜色渐变的直线？请尝试编写代码。

自己写

4、绘制圆和绘制椭圆的算法区别是什么？

自己写

5、在第一象限的四分之一椭圆弧上，切线斜率等于-1的点坐标是多少？

自己写

6、在绘制第一象限的四分之一椭圆弧时，如何判断像素点从切线斜率|k|<1的上半部分转入切线斜率|k|>1的下半部分？

自己写

六、实验总结

自己写

© 版权声明
文章版权归作者所有，未经允许请勿转载。如内容涉嫌侵权，请在本页底部进入<联系我们>进行举报投诉!
THE END
知识分享
如果内容对您有所帮助,就支持一下吧!
点赞0 分享
葡萄糖君的头像 - 宋马
河北省高级人民法院关于印发《破产案件审理规程》的通知 - 宋马
河北省高级人民法院关于印发《破产案件审理规程》的通知
河北省高级人民法院关于印发《破产案件审理规程》的通知
7个月前 49
网络录像机最常见问题通道“网络不可达”？一招教你解决！ - 宋马
网络录像机最常见问题通道“网络不可达”？一招教你解决！
网络录像机最常见问题通道“网络不可达”？一招教你解决！
3个月前 48
二维码批量生成工具 - 宋马
二维码批量生成工具
二维码批量生成工具
5个月前 42
豆包AI的图像处理技术：分割、擦除、重绘及扩展功能，免费无限次 - 宋马
豆包AI的图像处理技术：分割、擦除、重绘及扩展功能，免费无限次
豆包AI的图像处理技术：分割、擦除、重绘及扩展功能，免费无限次
2个月前 33
随机推荐
Windows 11自动熄屏设置全攻略：省电与便捷的完美平衡 - 宋马
Windows 11自动熄屏设置全攻略：省电与便捷的完美平衡
Windows 11自动熄屏设置全攻略：省电与便捷的完美平衡
4个月前 18
法考5轮背诵-宪法的解释体制 - 宋马
法考5轮背诵-宪法的解释体制
法考5轮背诵-宪法的解释体制
6个月前 11
CAD图纸加密软件是什么？到底要怎么加密CAD图纸呢？行内人教你3个诀窍！ - 宋马
CAD图纸加密软件是什么？到底要怎么加密CAD图纸呢？行内人教你3个诀窍！
CAD图纸加密软件是什么？到底要怎么加密CAD图纸呢？行内人教你3个诀窍！
6个月前 11
公路晒粮危害多，背后的安全隐患你真的知道吗? - 宋马
公路晒粮危害多，背后的安全隐患你真的知道吗?
公路晒粮危害多，背后的安全隐患你真的知道吗?
6个月前 18
《Python算法竞赛攻略：从入门到降维打击》——第五章 - 宋马
《Python算法竞赛攻略：从入门到降维打击》——第五章
《Python算法竞赛攻略：从入门到降维打击》——第五章
2个月前 9
门店活码，视频号小店引流企业微信私域的实用工具 - 宋马
门店活码，视频号小店引流企业微信私域的实用工具
门店活码，视频号小店引流企业微信私域的实用工具
1个月前 5
评论 抢沙发

请登录后发表评论

    暂无评论内容

用户封面
葡萄糖君的头像 - 宋马
豆包AI的图像处理技术：分割、擦除、重绘及扩展功能，免费无限次
网络录像机最常见问题通道“网络不可达”？一招教你解决！
河北省高级人民法院关于印发《破产案件审理规程》的通知
二维码批量生成工具
3个方法，教你如何设置 Windows 10/11 自动登录，一键直达桌面 - 宋马
1.2W+人已阅读
3个方法，教你如何设置 Windows 10/11 自动登录，一键直达桌面
TOP1
(番外)+(全文)李福海宋观潮：结局+全文+后续(李福海宋观潮)小说最新列表_官途风云李福海宋观潮：结局+全文+后续(李福海宋观潮)全文阅读无弹窗初官途风云：结局+全文+后续 - 宋马
(番外)+(全文)李福海宋观潮：结局+全文+后续(李福海宋观潮)小说最新列表_官途风云李福海宋观潮：结局+全文+后续(李福海宋观潮)全文阅读无弹窗初官途风云：结局+全文+后续
6个月前4224人已阅读
TOP2
热门视频《bj女团熊猫班全员卸甲》免费观看_《bj女团熊猫班全员卸甲》无删减版 HD 高清在线观看_《bj女团熊猫班全员卸甲》全集免费观看，《bj女团熊猫班全员卸甲》全集在线播放 - 西瓜影视网... - 宋马
热门视频《bj女团熊猫班全员卸甲》免费观看_《bj女团熊猫班全员卸甲》无删减版 HD 高清在线观看_《bj女团熊猫班全员卸甲》全集免费观看，《bj女团熊猫班全员卸甲》全集在线播放 – 西瓜影视网…
1个月前3856人已阅读
TOP3
QQ小世界突然消失！3亿用户炸锅：我的青春视频被一键清空了？ - 宋马
QQ小世界突然消失！3亿用户炸锅：我的青春视频被一键清空了？
5个月前3348人已阅读
TOP4
玩客云/网心云刷OpenWrt当旁路由教程 - 宋马
玩客云/网心云刷OpenWrt当旁路由教程
4个月前2815人已阅读
TOP5
最新困困兔宿舍录屏视频在线观看_宿舍直播回放完整版_高清原版网盘资源下载即点即看 - 宋马
最新困困兔宿舍录屏视频在线观看_宿舍直播回放完整版_高清原版网盘资源下载即点即看
1个月前2288人已阅读
TOP6
TOP1
TOP2
TOP3
TOP4
TOP5
TOP6
3个方法，教你如何设置 Windows 10/11 自动登录，一键直达桌面 - 宋马

3个方法，教你如何设置 Windows 10/11 自动登录，一键直达桌面

知识分享
般若如花的头像 - 宋马8个月前
41.2W+1
(番外)+(全文)李福海宋观潮：结局+全文+后续(李福海宋观潮)小说最新列表_官途风云李福海宋观潮：结局+全文+后续(李福海宋观潮)全文阅读无弹窗初官途风云：结局+全文+后续 - 宋马

(番外)+(全文)李福海宋观潮：结局+全文+后续(李福海宋观潮)小说最新列表_官途风云李福海宋观潮：结局+全文+后续(李福海宋观潮)全文阅读无弹窗初官途风云：结局+全文+后续

知识分享
会飞的龙的头像 - 宋马6个月前
042242
热门视频《bj女团熊猫班全员卸甲》免费观看_《bj女团熊猫班全员卸甲》无删减版 HD 高清在线观看_《bj女团熊猫班全员卸甲》全集免费观看，《bj女团熊猫班全员卸甲》全集在线播放 - 西瓜影视网... - 宋马

热门视频《bj女团熊猫班全员卸甲》免费观看_《bj女团熊猫班全员卸甲》无删减版 HD 高清在线观看_《bj女团熊猫班全员卸甲》全集免费观看，《bj女团熊猫班全员卸甲》全集在线播放 – 西瓜影视网…

知识分享
有梗回复的头像 - 宋马1个月前
038560
QQ小世界突然消失！3亿用户炸锅：我的青春视频被一键清空了？ - 宋马

QQ小世界突然消失！3亿用户炸锅：我的青春视频被一键清空了？

知识分享
我的云小姐的头像 - 宋马5个月前
233481
玩客云/网心云刷OpenWrt当旁路由教程 - 宋马

玩客云/网心云刷OpenWrt当旁路由教程

知识分享
多读书涨智慧的头像 - 宋马4个月前
028152
最新困困兔宿舍录屏视频在线观看_宿舍直播回放完整版_高清原版网盘资源下载即点即看 - 宋马

最新困困兔宿舍录屏视频在线观看_宿舍直播回放完整版_高清原版网盘资源下载即点即看

知识分享
轨迹的头像 - 宋马1个月前
022880
龚成思龙门县龙辉龙泉站龙族前传龙口市忠证基因龙口市亲子鉴定齐玉苓案鼻血的教训鼓励非公有制经济黔东南亲子鉴定机构黔东南亲子鉴定中心黔东南亲子鉴定黑龙江省长黑龙江省教育厅厅长黑龙江省司法厅黑话律师黑袍纠察队黑暗转向黑暗荣耀