【字节跳动】数据挖掘面试题0016：解释AUC的定义，它解决了什么问题，优缺点是什么，并说出工业界如何计算AUC。

文章大纲

AUC（Area Under the Curve）详解

一、定义：AUC是什么？
二、解决了什么问题？
三、优缺点分析
四、工业界大规模计算AUC的方法

1. 标准计算（小数据）
2. 工业级大规模计算方案
3.工业界最佳实践
4.工业界方案选型建议

总结：AUC的本质

AUC（Area Under the Curve）详解

一、定义：AUC是什么？

AUC是ROC曲线下的面积，用于衡量二分类模型性能的核心指标。

AUC的物理意义：

“随机抽一个正样本和一个负样本，正样本得分高于负样本的概率” —— 这正是工业界已关注排序能力的本质原因。

通俗解释：

想象两个袋子：

袋A：全是好苹果（正样本）
袋B：全是坏苹果（负样本）

你有一个苹果检测器（分类模型）：

随机从A袋拿一个好苹果
随机从B袋拿一个坏苹果
让检测器判断哪个是好苹果

AUC = 检测器做出正确判断的概率

AUC=1：每次都正确
AUC=0.5：和瞎猜一样
AUC<0.5：还不如瞎猜

技术定义：
A U C = P ( 正样本得分 > 负样本得分 ) AUC = P( ext{正样本得分} > ext{负样本得分}) AUC=P(正样本得分>负样本得分)
其中得分是 模型预测的"正类概率"

---

二、解决了什么问题？

不平衡数据评估难题

传统准确率在99%负样本的数据中失效（全预测负类就有99%准确率）
AUC不受样本分布影响

分类阈值选择问题

不需要预先设定分类阈值（如0.5）
评估模型在所有阈值下的综合表现

模型排序能力评估

直接衡量”把正样本排在负样本前面”的能力
这对 推荐系统/风控 等场景至关重要

---

三、优缺点分析

优点	缺点
不受类别分布影响	无法反映具体错误代价
直观的概率解释	对类别概率校准不敏感
评估模型整体排序能力	计算复杂度较高
广泛适用于不同场景	无法区分不同”错误类型”（如FP/FN）
与业务目标高度相关	对预测分数尺度不敏感

特殊注意：

AUC高 ≠ 模型有用： 当负样本极易区分时（如身高判断性别），AUC虚高
AUC低一定差：低于0.5说明模型存在根本缺陷

---

四、工业界大规模计算AUC的方法

1. 标准计算（小数据）

from sklearn.metrics import roc_auc_score

auc = roc_auc_score(y_true, y_pred)

局限：需加载全量数据到内存，100亿数据直接崩溃

2. 工业级大规模计算方案

方案一：分桶近似法（最常用，Bucket Approximation，按分数段统计胜场（近似））

适用场景： 超大数据集（百亿级）、需平衡精度与速度 。

桶数量决定精度（工业界常用10万-100万桶）

核心思想： 将预测概率分桶 → 统计桶内正负样本数 → 用梯形面积累加近似AUC。

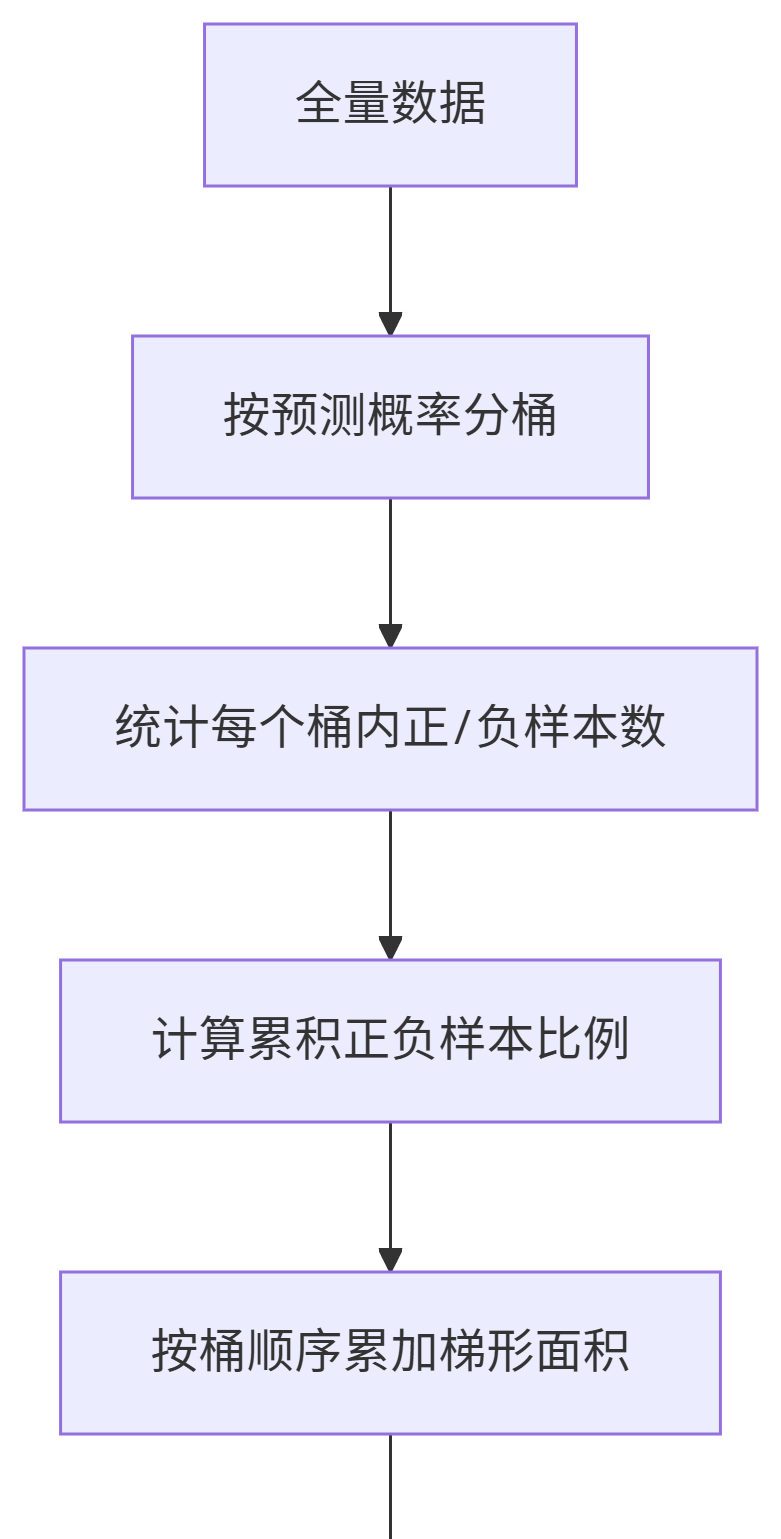
def approximate_auc(y_true, y_pred, n_buckets=10000):
    # 将预测分数分桶
    buckets = np.linspace(0, 1, n_buckets)
    bucket_stats = np.zeros((n_buckets, 2))  # [正样本数, 负样本数]
    
    # 分布式统计每个桶的正负样本数
    for i in range(len(y_pred)):
        bucket_idx = np.searchsorted(buckets, y_pred[i])
        if y_true[i] == 1:
            bucket_stats[bucket_idx, 0] += 1
        else:
            bucket_stats[bucket_idx, 1] += 1
    
    # 计算AUC（梯形面积法）
    auc = 0
    cum_neg = 0
    total_pos = bucket_stats[:, 0].sum()
    
    for i in range(n_buckets):
        num_pos = bucket_stats[i, 0]
        num_neg = bucket_stats[i, 1]
        auc += num_pos * (cum_neg + 0.5 * num_neg)
        cum_neg += num_neg
    
    return auc / (total_pos * cum_neg)

关键实现：

分桶技巧：桶数量（如10万桶）影响精度，桶越多越准但计算越慢。
分布式优化：用MapReduce统计桶内数据，避免单机内存瓶颈。
公式：
AUC = ∑ i ( cum_neg i × pos i + 0.5 × neg i × pos i ) 总正样本 × 总负样本 ext{AUC} = frac{sum_{i} ( ext{cum\_neg}_i imes ext{pos}_i + 0.5 imes ext{neg}_i imes ext{pos}_i)}{ ext{总正样本} imes ext{总负样本}} AUC=总正样本×总负样本∑i​(cum_negi​×posi​+0.5×negi​×posi​)​
（cum_neg_i：第i桶前累积负样本数）。

物理意义解释： 想象把学生按考试成绩从低到高分成10个等级（桶）：

第5等级（桶）有3名优秀生（正样本）和2名普通生（负样本）
前4个等级共有15名普通生（cum_neg_i）
优秀生肯定比前4等级所有普通生成绩好 → 3×15=45分
同等级内优秀生有50%概率比普通生成绩好 → 0.5×3×2=3分
该桶贡献：45+3=48分
最终AUC = 所有桶总分 / (总优秀生×总普通生)

---

方案二：分布式排序法（Spark等，用排名精确计算胜场）

适用场景：需精确AUC、集群资源充足。
核心思想：

全局排序样本得分 → 正样本的排名和决定AUC（公式： AUC = ∑ 正样本排名 − 正样本数 ( 正样本数 + 1 ) 2 正样本数 × 负样本数 ext{AUC} = frac{sum ext{正样本排名} – frac{ ext{正样本数}( ext{正样本数}+1)}{2}}{ ext{正样本数} imes ext{负样本数}} AUC=正样本数×负样本数∑正样本排名−2正样本数(正样本数+1)​​）。

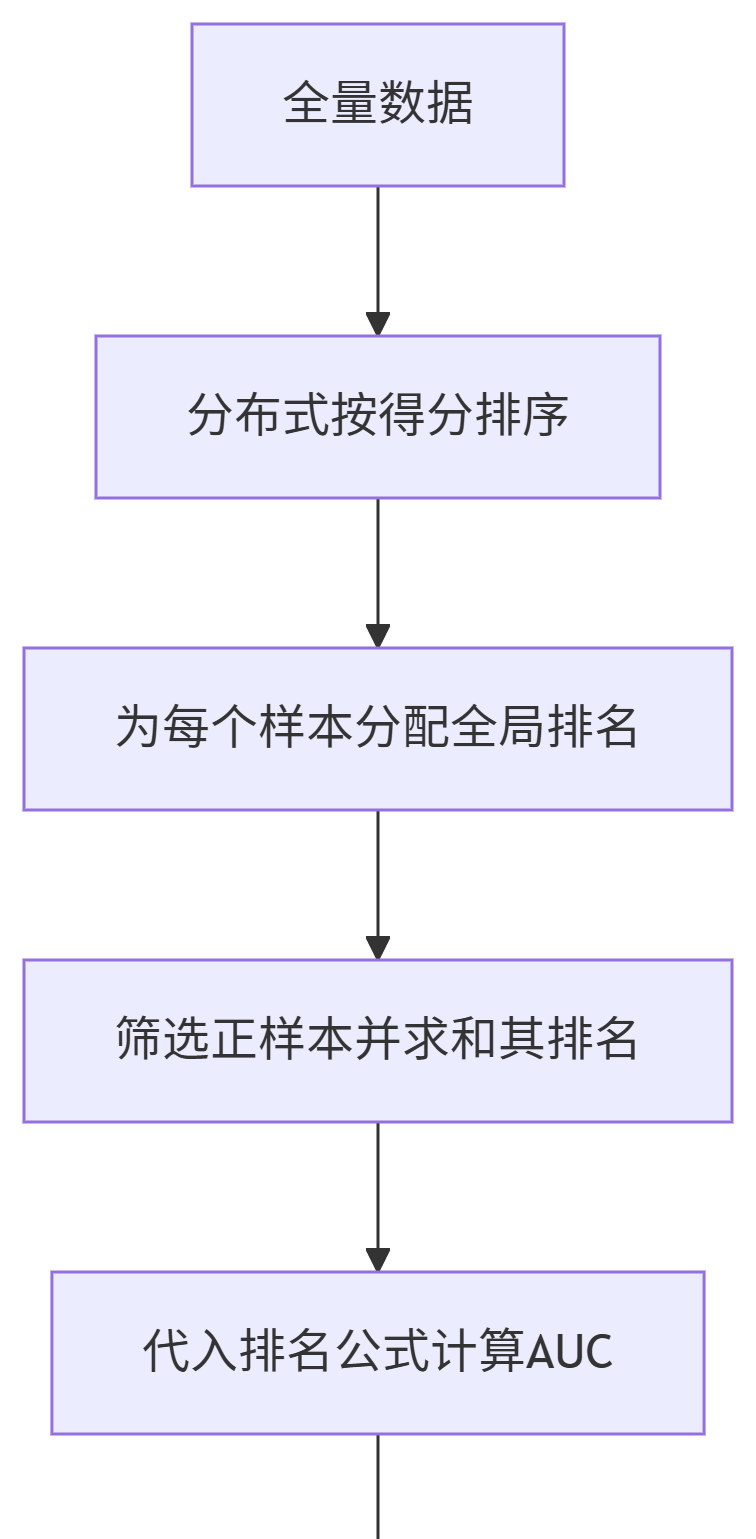
关键实现：

排序优化：用Spark的sortByKey+zipWithIndex分布式生成排名。
公式推导：
AUC = S − P ( P + 1 ) 2 P × N ext{AUC} = frac{S – frac{P(P+1)}{2}}{P imes N} AUC=P×NS−2P(P+1)​​
（S：正样本排名和；P：正样本数；N：负样本数）。

物理意义解释：
假设10个学生按成绩排序：

	排名：1  2  3  4  5  6  7  8  9  10
	标签：负 负 正 负 正 负 正 负 正 负

正样本（优秀生）位置：3,5,7,9
排名和S=3+5+7+9=24
正样本数P=4
调整项：P(P+1)/2 = 4×5/2=10（正样本间相互比较的次数）
有效比较分=24-10=14
总可能比较对数=4×6=24
AUC=14/24≈0.583

// Spark实现（内存优化版）
val predictions: RDD[(Double, Double)] = ... // (score, label)

val sortedData = predictions.sortByKey()
val numPos = sortedData.filter(_._2 == 1).count()
val numNeg = sortedData.count() - numPos

// 计算排名和
val rankSum = sortedData.zipWithIndex()
  .filter {
                   case ((_, label), _) => label == 1 }
  .map {
                   case ((_, _), index) => index + 1 }
  .sum()

val auc = (rankSum - numPos*(numPos+1)/2.0) / (numPos * numNeg)

方案三：流式计算（实时AUC，随机PK估算胜率）

适用场景： 快速估算、实时监控场景。
核心思想： 随机采样正负样本对 → 统计正样本得分 > 负样本得分的比例。

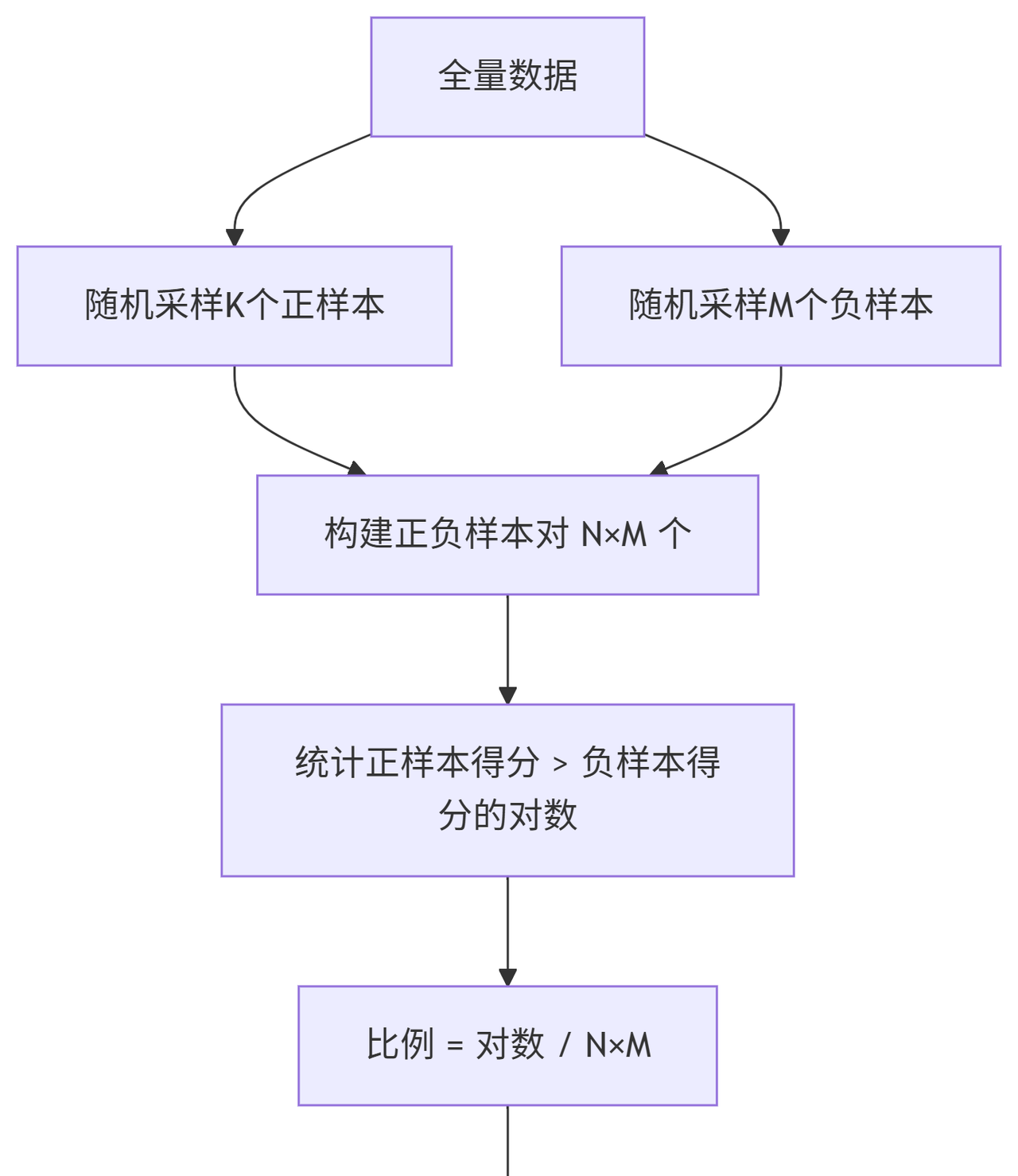
class StreamingAUC:
    def __init__(self, reservoir_size=100000):
        self.reservoir = []  # 蓄水池采样
        self.reservoir_size = reservoir_size
        self.count = 0
    
    def update(self, score, label):
        # 蓄水池采样维持固定样本量
        if len(self.reservoir) < self.reservoir_size:
            self.reservoir.append((score, label))
        else:
            idx = random.randint(0, self.count)
            if idx < self.reservoir_size:
                self.reservoir[idx] = (score, label)
        self.count += 1
    
    def get_auc(self):
        # 用采样样本计算近似AUC
        return roc_auc_score(
            [label for (_, label) in self.reservoir],
            [score for (score, _) in self.reservoir]
        )

关键实现：

采样量：通常10^6–107对（精度±0.01）。
分布式加速：用Spark的cartesian算子生成样本对并行计算。

---

3.工业界最佳实践

100亿级数据：

使用分桶法（10万-100万桶）
分布式计算（Spark/Dask）
误差控制在0.001内

实时监控场景：

蓄水池采样 + 滑动窗口
每小时全量计算一次校准

算法优化技巧：

# 计算加速技巧（避免全排序）
def fast_auc(y_true, y_pred):
    pos = y_pred[y_true == 1]
    neg = y_pred[y_true == 0]
    return (pos[:, None] > neg).mean()  # 向量化比较

业务适配建议：

广告推荐：已关注top10%的AUC（业务相关AUC）
风控系统：分段计算AUC（高中低风险区）

---

4.工业界方案选型建议

场景	推荐方案	原因	精度/速度
百亿数据+离线计算	分桶法	内存高效，精度可控	精度中高，速度快
高精度要求+集群资源充足	分布式排序法	结果精确	精度高，速度慢
实时监控/快速迭代	正负样本对采样法	最快，可流式更新	精度低，速度极快

💡 实用技巧：在Spark中，分桶法可用approxQuantile分桶+reduceByKey统计；采样法用sample+cartesian。

总结：AUC的本质

AUC衡量的是模型对”谁更好”的判断能力

在推荐系统：能否把用户喜欢的排在不喜欢的之前
在风控系统：能否把高风险排在低风险之前
在医疗诊断：能否把病人排在健康人之前

---

正是这种 对"排序能力"的量化，使AUC成为工业界不可替代的评估指标。
大规模计算的核心思路是：分而治之 + 近似估计，通过分布式计算和抽样技术平衡精度与效率。