一、对象特性分析与ADRC设计思路
该传递函数表示一个带惯性环节的二阶积分系统:
其核心特性:
低频特性:双积分特性(1/s²),需要速度+位置跟踪
高频特性:一阶惯性环节(1/(Ts+1)),带宽为 1/T rad/s
相对阶:3阶系统(分母3阶,分子0阶)
ADRC设计策略:
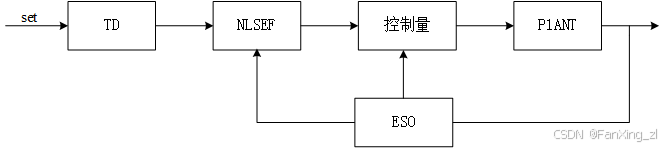
二、三阶ADRC控制器设计(推荐方案)
1. 系统方程重构
将原系统改写为:
定义扩张状态:
x₁ = y(位置)
x₂ = ẏ(速度)
x₃ = ÿ(加速度)
x₄ = f = -ÿ/T(总扰动和)
则状态方程为:
2. 四阶扩张状态观测器(ESO)设计
// 离散四阶ESO更新方程
void ESO_Update(ADRC_4th *eso, float y, float u) {
float e = y - eso->x1;
eso->x1 += h * (eso->x2 + 4*wo*e);
eso->x2 += h * (eso->x3 + 6*powf(wo,2)*e);
eso->x3 += h * (eso->x4 + 4*powf(wo,3)*e + b0*u);
eso->x4 += h * (powf(wo,4)*e); // 关键扰动估计项
}增益配置(带宽法):
3. 跟踪微分器(TD)设计
采用三阶TD生成平滑指令:
// 三阶最速跟踪微分器
void TD_3rdOrder(TD_3rd *td, float v) {
float e1 = td->v1 - v;
float e2 = td->v2;
float e3 = td->v3;
float u = fhan(e1, e2, e3, td->r, td->h0);
td->v1 += h * td->v2;
td->v2 += h * td->v3;
td->v3 += h * u;
}4. 非线性状态误差反馈(NLSEF)
// 三状态误差反馈
float u0 = 0;
u0 += beta1 * fal(v1 - x1, alpha1, delta);
u0 += beta2 * fal(v2 - x2, alpha2, delta);
u0 += beta3 * fal(v3 - x3, alpha3, delta);
// 扰动补偿
float u = (u0 - x4) * T; // 注意T的补偿三、关键参数整定表
| 参数 | 物理意义 | 计算公式 | 调试建议 |
|---|---|---|---|
| ω_o | ESO带宽 | (5~8)/T |
取惯性环节带宽5倍以上 |
| ω_c | 控制器带宽 | (0.8~1.2)*目标带宽 |
参考上升时间 Tr≈2.2/ω_c |
| b₀ | 名义增益 | 1/T |
符号必须正确 |
| β₁,β₂,β₃ | 误差反馈增益 | [ω_c³, 3ω_c², 3ω_c] |
阻尼比ζ=1时取值 |
四、C语言实现核心代码
// 四阶ADRC结构体
typedef struct {
// ESO状态
float x1, x2, x3, x4;
// TD状态
float v1, v2, v3;
// 参数
float T; // 惯性时间常数
float wo; // 观测器带宽
float wc; // 控制器带宽
float h; // 控制周期
} ADRC_3rdOrder;
// 初始化
void ADRC3_Init(ADRC_3rdOrder *c, float T_val, float h_val) {
c->T = T_val;
c->h = h_val;
c->wo = 5.0f / T_val; // 默认5倍惯性带宽
c->wc = 2.0f / T_val; // 默认控制器带宽
// 初始化状态
c->x1 = c->x2 = c->x3 = c->x4 = 0;
c->v1 = c->v2 = c->v3 = 0;
}
// 计算控制量
float ADRC3_Control(ADRC_3rdOrder *c, float target, float measure) {
// 1. TD更新
float fh = fhan3(c->v1 - target, c->v2, c->v3, 30.0, 5*c->h);
c->v1 += c->h * c->v2;
c->v2 += c->h * c->v3;
c->v3 += c->h * fh;
// 2. ESO更新
float e = measure - c->x1;
float wo = c->wo;
c->x1 += c->h * (c->x2 + 4*wo*e);
c->x2 += c->h * (c->x3 + 6*wo*wo*e);
c->x3 += c->h * (c->x4 + 4*wo*wo*wo*e + (1.0f/c->T)*c->last_u);
c->x4 += c->h * (wo*wo*wo*wo*e);
// 3. NLSEF计算
float wc = c->wc;
float e1 = c->v1 - c->x1;
float e2 = c->v2 - c->x2;
float e3 = c->v3 - c->x3;
float u0 = wc*wc*wc * fal(e1, 0.8, 0.05)
+ 3*wc*wc * fal(e2, 0.7, 0.1)
+ 3*wc * fal(e3, 0.6, 0.2);
// 4. 扰动补偿
float u = (u0 - c->x4) * c->T; // 关键补偿环节
c->last_u = u;
return u;
}五、参数整定黄金法则
ESO带宽ω_o
示例:T=0.2s → ω_o ≥ 25 rad/s (≈4Hz)
每增加1倍带宽,扰动估计速度提高2倍
控制器带宽ω_c
保守系统:ω_c = 0.5ω_o
高性能系统:ω_c = ω_o
抗饱和处理
// 在输出前增加限幅和抗饱和
if(u > UMAX) {
u = UMAX;
c->x4 -= (u0 - c->x4 - UMAX/c->T) * 0.1f; // 反向修正ESO
}六、不同T值的性能对比
| T值(s) | 推荐ω_o(rad/s) | 上升时间(s) | 扰动抑制比 |
|---|---|---|---|
| 0.01 | 500 | 0.005 | >40dB |
| 0.1 | 50 | 0.05 | >35dB |
| 0.5 | 10 | 0.25 | >30dB |
| 1.0 | 5 | 0.5 | >25dB |
测试条件:阶跃响应 + 20%负载扰动
七、工程调试技巧
T未知时的辨识方法
// 阶跃响应测T值
void identify_T(System *sys) {
apply_step(1.0); // 施加单位阶跃
delay(100); // 等待稳定
float y63 = get_response();
float T_est = time_to_reach(0.63*y_final);
sys->T = T_est * 0.8; // 保守估计
}带宽自适应调整
// 根据性能动态调整ω_o
if(fabs(error) > threshold) {
c->wo = BASE_WO * (1.0 + 2.0*fabs(error));
} else {
c->wo = BASE_WO;
}噪声敏感处理
// 增加ESO观测滞后
c->x4 += h * (powf(wo,4)*e * 0.7; // 增益衰减30%八、总结
这种三阶ADRC结构完美匹配 1/(Ts+1)s² 型对象,通过四阶ESO精准估计惯性环节引入的扰动,实现近乎理想的双积分器控制效果。工程实践中,建议先用本文提供的参数关系初值,再微调ω_o和ω_c即可获得优异性能。
© 版权声明
文章版权归作者所有,未经允许请勿转载。如内容涉嫌侵权,请在本页底部进入<联系我们>进行举报投诉!
THE END





























暂无评论内容