
引用格式 :Lakshminarayanan B, Pritzel A, Blundell C. Simple and scalable predictive uncertainty estimation using deep ensembles[J]. Advances in neural information processing systems, 2017, 30.
引用量:5882
使用深度集成的方法进行简单和可扩展的预测不确定性估计
3 Experimental results
3.1 Evaluation metrics and experimental setup
对于分类和回归,我们评估了依赖于预测不确定性的负对数似然(NLL)。NLL是一种合适的评分规则,也是评估预测不确定性的常用指标[49]。对于分类,我们还测量分类精度和Brier score,定义为




[49] J. Quinonero-Candela, C. E. Rasmussen, F. Sinz, O. Bousquet, and B. Scholkopf. Evaluating predictive uncertainty challenge. In Machine Learning Challenges. Springer, 2006.
3.2 Regression on toy datasets
首先,我们在一维toy回归数据集上定性地评估了所提出方法的性能。该数据集由Hernandez-Lobato和Adams[24]使用,由20个训练样例组成,绘制为,其中

实践中常用的启发式方法是使用神经网络的集合(经过训练以最小化MSE),获得多点预测,并使用网络预测的经验方差作为不确定性的近似度量。我们证明,这不如使用NLL训练来学习方差(参见附录A.2获取真实数据集的校准结果)。结果如图1所示。
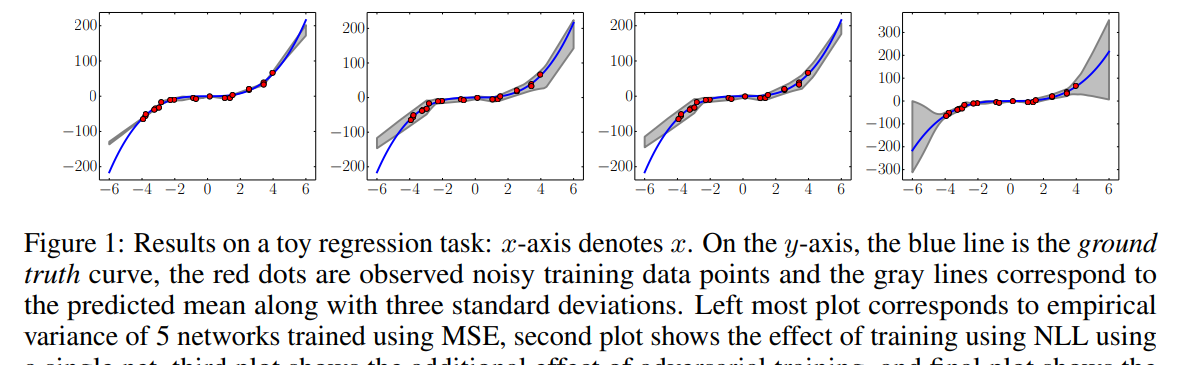
图1:toy回归任务的结果:x轴表示x。在y轴上,蓝线为真实值曲线,红点为观察到的有噪声的训练数据点,灰线对应预测平均值和三个标准差。最左边的图对应使用MSE训练的5个网络的经验方差,第二个图表示使用单个网络使用NLL训练的效果,第三个图表示使用对抗训练的附加效果,最后一个图表示分别使用5个网络的集合的效果。
结果清楚地表明:(i)使用评分规则(NLL)学习方差和训练可以改善预测不确定性,(ii)集成组合可以提高性能,特别是当我们远离观察到的训练数据时。
3.3 Regression on real world datasets
在我们的下一个实验中,我们将我们的方法与在回归任务中使用神经网络进行预测不确定性估计的最先进方法进行比较。我们使用Hernandez- Lobato和Adams[24]提出的实验设置来评估概率反向传播(PBP),该实验也被Gal和Ghahramani[15]使用来评价mc -dropout(我们没有比较VI[19],因为PBP和MC-dropout在这些基准上优于VI。)。每个数据集被分成20个训练测试折叠(train-test folds),除了蛋白质数据集(protein dataset)使用5个折叠和年份预测MSD数据集(Year Prediction MSD dataset)使用单个训练测试分割。我们使用相同的网络架构:具有ReLU非线性的1个隐藏层神经网络[45],对于较小的数据集包含50个隐藏单元,对于较大的蛋白质和年份预测MSD数据集包含100个隐藏单元。我们训练了40个epoch;关于数据集和实验方案的更多细节,我们参考[24]。我们在集成中使用了5个网络。我们的结果显示在表1中,以及报告了各自论文中的PBP和MC-dropout结果。
[45] V. Nair and G. E. Hinton. Rectified linear units improve restricted Boltzmann machines. In ICML, 2010.
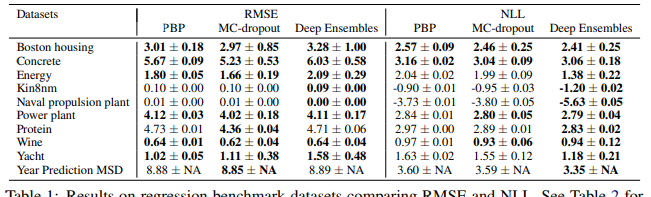
表1:在回归基准数据集上比较RMSE和NLL的结果。我们方法的变体结果见表2。
我们观察到,我们的方法在NLL方面优于(或与)现有方法。在一些数据集上,我们观察到我们的方法在RMSE方面稍微差一些。我们认为这是因为我们的方法针对NLL(捕获预测不确定性)而不是MSE进行了优化。附录A.1中的表2报告了我们方法变体的其他结果,展示了使用集成和学习方差的优势。
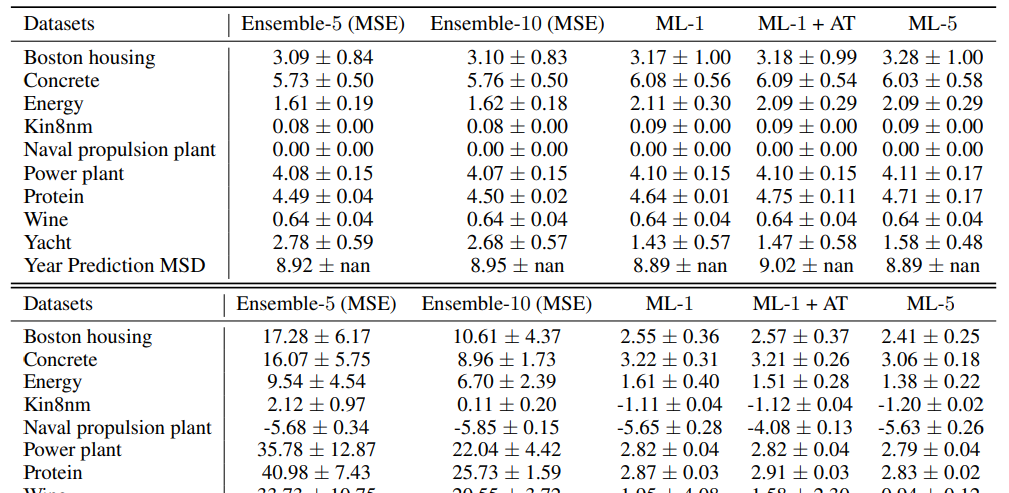
表2:回归基准数据集的其他结果:上表报告RMSE,下表报告NLL。ensemble -M (MSE)表示经过训练以最小化均方误差(MSE)的M个网络的集合;预测方差是单个网络预测的经验方差。ML-1表示在2.2.1节中描述的单个网络训练预测均值和方差的最大似然。ML-1显著优于ensembles -5 (MSE)和ensembles -10 (MSE),清楚地表明学习方差的影响。ML-1+AT表示对抗训练(AT)的额外效果;AT在这些基准测试中没有显著的帮助。ML-5,在表1中称为深度集成,是一个由5个网络组成的集成,经过训练可以预测均值和方差。ML-5+AT的结果与ML-5非常相似(误差条重叠),因此我们不在这里报告它们。
3.4 Classification on MNIST, SVHN and ImageNet
接下来,我们使用MNIST和SVHN数据集评估分类任务的性能。我们的目标不是在这些问题上实现最先进的性能,而是评估对抗性训练的效果以及集合中网络的数量。为了验证对抗性训练是否有帮助,我们还包括一个基线,它选择一个随机的有符号向量。对于MNIST,我们使用具有3个隐藏层的MLP,每层有200个隐藏单元,以及具有批处理归一化的ReLU非线性。对于MC-dropout,我们在每个非线性之后添加dropout, dropout率为0.1(我们也尝试了0.5的dropout,但效果更差。)。结果如图2(a)所示。我们观察到,对抗训练和增加集合中网络的数量显著提高了分类精度以及NLL和Brier score的性能,这表明我们的方法产生了校准良好的不确定性估计。对抗训练比随机方向的增强训练能带来更好的表现。我们的方法在所有性能指标上也比MC-dropout要好得多。请注意,用不变性(如随机裁剪和水平翻转)增强训练数据集是对抗性训练的补充,可以潜在地提高性能。
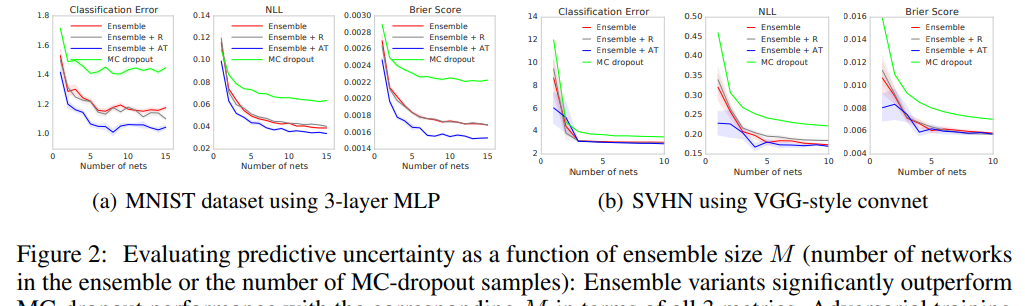
图2:集成尺寸大小为M预测不确定性(M为集成中的网络数量或MC-dropout样本数量)的函数进行评估:就所有3个指标而言,具有相应M的集成变量显著优于MC-dropout性能。当M = 1时,对抗性训练提高了MNIST对所有M和SVHN的结果,但效果随着M的增加而下降。
为了测量结果对网络结构选择的敏感性,我们实验了一个双层MLP和一个卷积神经网络;我们观察到定性相似的结果;详见附录B.1。
我们还使用VGG风格的卷积NN报告了SVHN数据集的结果(该体系结构类似于http://torch.ch/blog/2015/07/30/cifar.html中描述的体系结构。)。结果见图2(b)。集成的表现优于MC-dropout。当M = 1时,对抗性训练略有帮助,但随着集合中网络数量的增加,效果会下降。如果分类分离得很好,对抗性训练可能不会显著改变分类边界。目前尚不清楚这里的情况是否如此,需要进一步调查。
最后,我们在ImageNet (ILSVRC-2012)数据集[51]上使用初始网络[56]进行评估。由于计算限制,我们只评估集成对该数据集的影响。在ImageNet(单作物评估)上的结果如表4所示。我们观察到,随着M的增加,预测不确定性的准确性和质量都有显著提高。
[51] O. Russakovsky, J. Deng, H. Su, J. Krause, S. Satheesh, S. Ma, Z. Huang, A. Karpathy, A. Khosla, M. Bernstein, A. C. Berg, and L. Fei-Fei. ImageNet Large Scale Visual Recognition Challenge. International Journal of Computer Vision (IJCV), 115(3):211–252, 2015.
[56] C. Szegedy, V. Vanhoucke, S. Ioffe, J. Shlens, and Z. Wojna. Rethinking the inception architecture for computer vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 2818–2826, 2016.
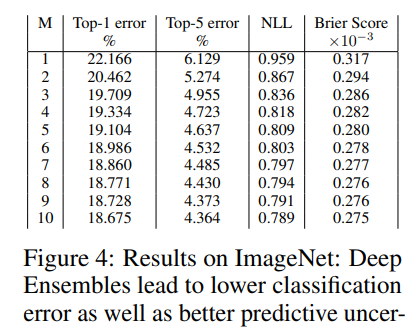
图4:ImageNet上的结果:从较低的NLL和Brier评分可以看出,Deep Ensembles的分类误差较低,预测不确定性也较好。
使用集成的另一个优点是,它使我们能够轻松地识别单个网络不一致或最一致的训练示例。这种分歧(更准确地说,我们将不一致定义为


图10:MNIST上的结果显示了集成中网络之间有高或低分歧的测试样例:上面两行表示分歧最小的测试样例,下面两行表示分歧最大的测试样例。

图11:MNIST上显示高置信度或低置信度的测试示例的结果:顶部两行表示具有最高置信度的测试示例,底部两行表示具有最低置信度的测试示例。
3.5 Uncertainty evaluation: test examples from known vs unknown classes
在最后的实验中,我们评估了未见过的类的分布外示例的不确定性。对未知类的过度自信的预测对在现实世界应用中可靠地部署深度学习模型构成了挑战。当测试数据与训练数据非常不同时,我们希望预测显示出更高的不确定性。为了测试所提出的方法是否具有这种理想的特性,我们使用与以前相同的架构在标准MNIST训练/测试分割上训练MLP。然而,除了具有已知类的常规测试集之外,我们还在包含未知类的测试集上对其进行评估。我们使用NotMNIST(可在http://yaroslavvb.blogspot.co.uk/2011/09/notmnist-dataset.html下载)数据集的测试分割。该数据集中的图像与MNIST具有相同的大小,但是标签是字母而不是数字。我们无法获得真实的条件概率,但我们期望与已知类相比,未知类的预测更接近均匀,在已知类中,预测概率应该集中在真实目标上。我们评估预测分布的熵,并用它来评估不确定性估计的质量。结果如图3(a)所示。对于已知的类(上一行),我们的方法和MC-dropout都具有预期的低熵。对于未知类(下一行),随着M的增加,深度集成的熵增加得比MC-dropout快得多,这表明我们的方法更适合处理看不见的测试示例。特别是,MC-dropout似乎对一些测试例子给出了高置信度的预测,即使是看不见的类别,其模式也在0左右。在实践中,当在已知类和未知类的混合上进行测试时,这种过于自信的错误预测可能会产生问题,我们将在3.6节中看到。比较我们方法的不同变体,对抗训练模式的增长速度略快于香草集成模式,这表明对抗训练用于量化未知类的不确定性是有益的。我们对附录B .2中图12(a)和图12(b)中的结果进行定性评价。图12(a)显示,字母“I”与MNIST训练数据集中的1相似时,集成一致性最高,而对于视觉上与MNIST训练数据集中不同的示例,集成一致性更高。
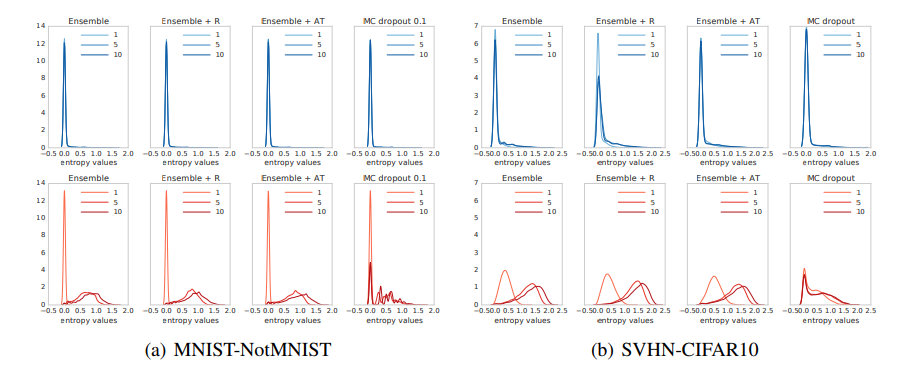
图3:当我们改变集合大小M时,来自已知类(上一行)和未知类(下一行)的测试样本的预测熵的直方图。

图12:在MNIST上训练的深度集成和在包含未见类的NotMNIST数据集上测试的深度集成:在左边,最上面的两行表示具有最高置信度的测试示例,最下面的两行表示具有最低置信度的测试示例。在右边,最上面的两行表示置信度最高的测试示例,最下面的两行表示置信度最低的测试示例。我们观察到这些措施捕获了有意义的歧义:例如,字母“I”和一些类似于MNIST训练数据集中的“J”变体的集成一致性很高。对于视觉上与MNIST训练数据集不相似的例子,集成分歧很大,置信度很低。
我们进行了类似的实验,在SVHN上进行训练,在CIFAR-10[31]测试集上进行测试;两个数据集都包含32 × 32 × 3的图像,但SVHN包含数字图像,而CIFAR-10包含对象类别图像。结果如图3(b)所示。正如在MNIST-NotMNIST实验中,我们观察到MC-dropout在未见过的例子上产生了过度自信的预测,而我们的方法在未见过的类别上产生了更高的不确定性。
[31] A. Krizhevsky. Learning multiple layers of features from tiny images. 2009.
最后,我们在ImageNet上通过按类别划分训练集进行测试。我们将数据集分成狗(已知类别)和非狗(未知类别)的图像,遵循Vinyals等人[58]为不同任务提出的这种设置。图5显示了预测熵的直方图以及最大预测概率(即预测类的置信度)。我们观察到,随着集合大小的增加,预测不确定性在未见的类别上有所提高。
[58] O. Vinyals, C. Blundell, T. Lillicrap, D. Wierstra, et al. Matching networks for one shot learning. In NIPS, 2016.
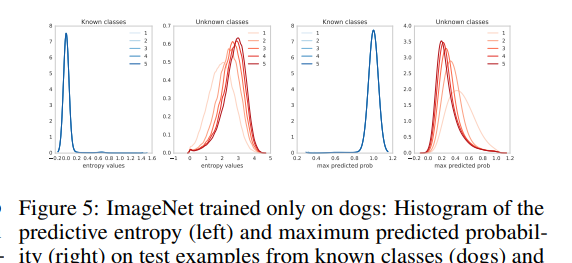
图5:仅对狗进行训练的ImageNet:在我们改变集合大小时,来自已知类别(狗)和未知类别(非狗)的测试示例的预测熵(左)和最大预测概率(右)的直方图。
3.6 Accuracy as a function of confidence
在实际应用中,非常希望系统能够避免过度自信、不正确的预测和优雅地失败。为了评估预测不确定性对决策的有用性,我们考虑一个任务,其中模型仅在模型置信度高于用户指定阈值的情况下进行评估。如果置信度估计校准得很好,当报告的置信度很高时,人们可以相信模型的预测,而当模型不自信时,可以采用不同的解决方案(例如,在循环中使用人,或使用来自更简单模型的预测)。
我们重用上一节中的实验结果,我们在MNIST上训练了一个网络,并在MNIST(已知类)和NotMNIST(未知类)的混合测试示例上对其进行测试。网络将对分布外的例子产生不正确的预测,然而我们希望这些预测具有低置信度。给定预测


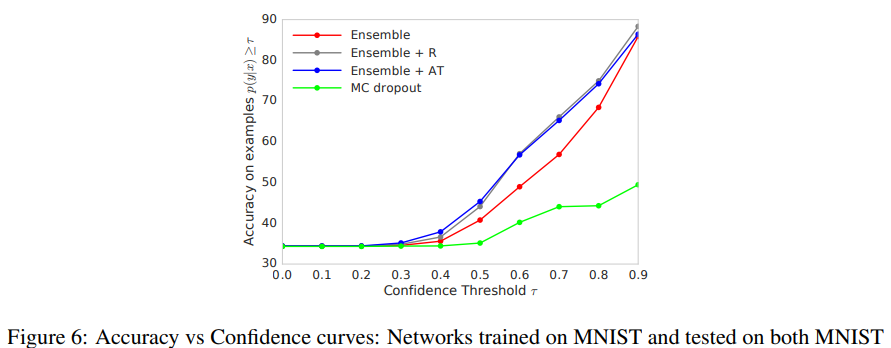
图6:准确度与置信度曲线:网络在MNIST上训练,并在包含已知类的MNIST测试和包含未知类的NotMNIST数据集上进行测试。MC-dropout可能产生过于自信的错误预测,而深度集成则明显更加稳健。






















暂无评论内容