Gmsh 使用入门：网格拉伸与设置周期边界

一、引言

Gmsh是著名的开源3D有限元网格生成器，简单易用但功能强劲，之前我们已经写过一些文章对Gmsh的基础功能进行介绍，可以参考：Gmsh使用入门: 构建几何模型、Gmsh使用入门：网格生成。

本文将对Gmsh的更多功能进行介绍，包括Gmsh中的网格拉伸功能，以及如何设置周期边界。

二、网格拉伸

Gmsh中支持通过类似拉伸（扫掠）的方式，使用gmsh.model.occ.extrude函数，将更低维的几何实体拉伸为更高维的几何实体，即将点拉伸成线，线拉伸成面，或者将面拉伸成体：

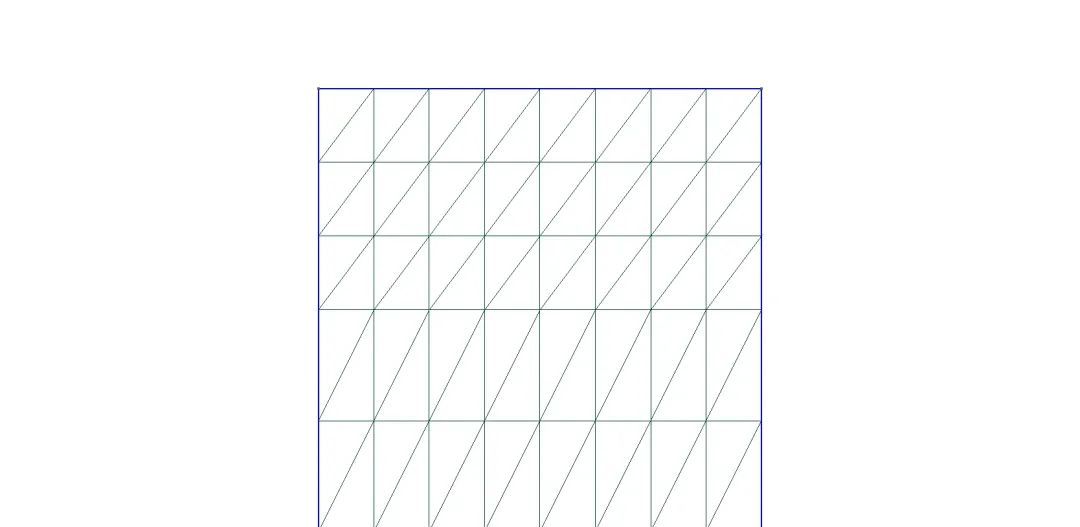
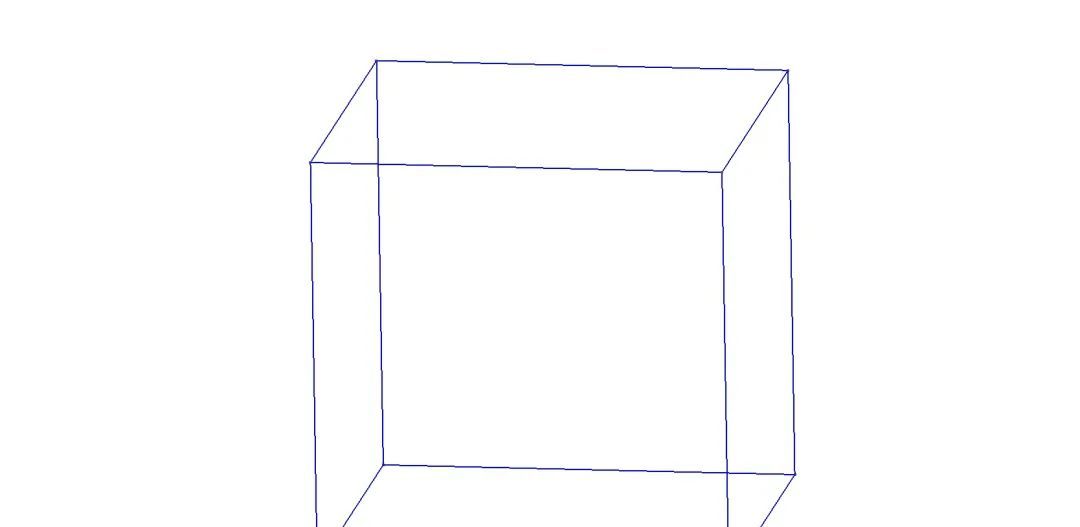
gmsh.model.occ.extrude函数的参数列表如下：

def extrude(dimTags, dx, dy, dz, numElements=[], heights=[], recombine=False):

其中：

以一个box为例，如果不指定后续三个参数，依旧可以将低维的几何实体拉伸成更高维的几何实体，但是并不会有分层的结构，只会在拉伸后的几何区域中直接生成网格：

当我们指定了numElements以及heights，recombine设置为False，生成的是分层的四面体网格：

如果进一步将recombine设置为True，会尝试将四面体网格重组为三棱柱网格：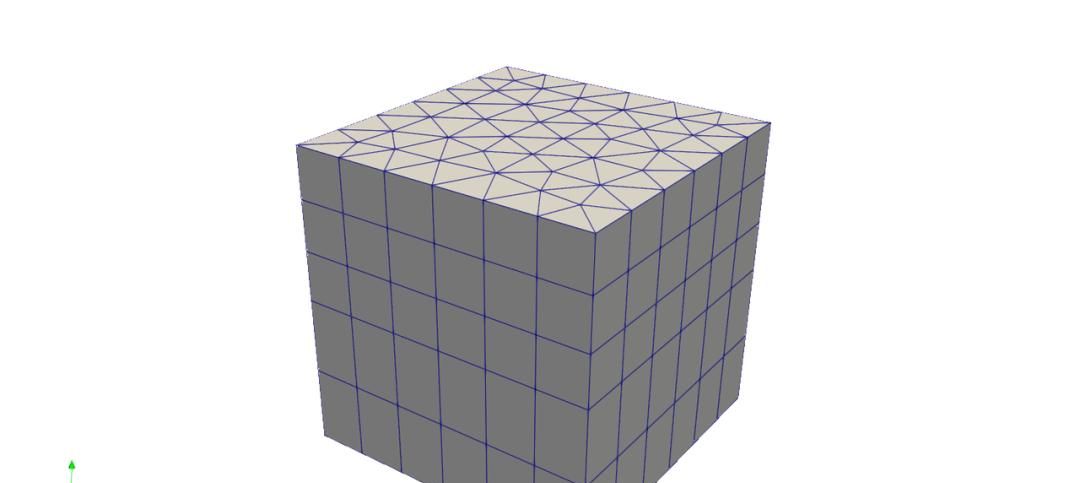

但是当不指定numElements以及heights，仅仅将recombine设置为True，生成的依旧是四面体网格，由于没有明确的分层结构，Gmsh无法将四面体网格重组为三棱柱网格。

三、周期边界

周期边界条件：在有限元方法中，周期边界条件（Periodic Boundary Conditions, PBCs）是一种特殊的边界条件，用于模拟具有周期性结构的物理问题。周期边界条件一般成对出现，在周期边界上，物理量满足周期性关系，因此要求周期边界上的几何结构保持一致，相应的网格也需要一致。

Gmsh可以通过gmsh.model.mesh.setPeriodic函数方便地设置周期边界，其本质是先在控制实体（master）上生成网格，再将控制实体生成的网格复制到周期实体上：

def setPeriodic(dim, tags, tagsMaster, affineTransform):

其中：

1.dim：周期实体的几何维数；

2.tags：周期实体的标签列表；

3.tagsMaster：控制实体标签列表；

4.affineTransform：长度为16的列表，对应于的仿射变换矩阵，定义控制实体到周期实体的变换。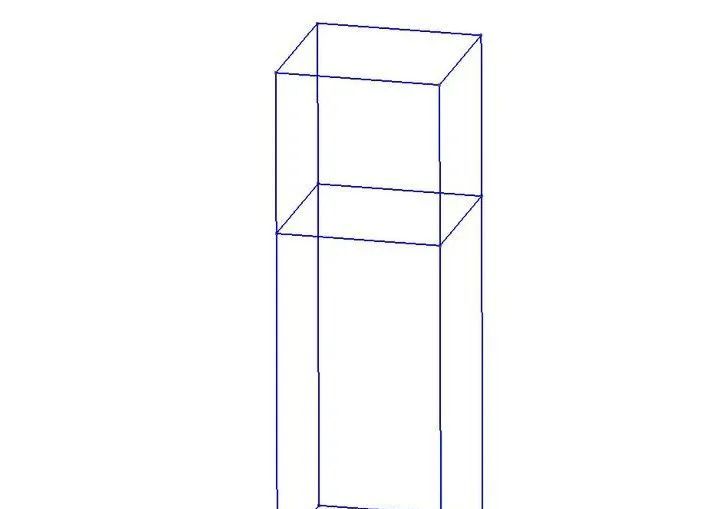

举个例子，对于下面的几何对象：

其由两个长方体组成，长、宽都为1，高分别为2和1，由如下代码生成：

lx, ly, lz = 1.0, 1.0, 2.0
# 创建box
box1 = gmsh.model.occ.addBox(0, 0, 0, lx, ly, lz)
box2 = gmsh.model.occ.addBox(0, 0, lz, lx, ly, lz/2)
box = gmsh.model.occ.fragment([(3, box1)], [(3, box2)], removeObject=True)[0][0]

想要设置该几何实体的方向的面（面标签为2和8），以及方向的面（面标签为1和7）为周期边界，可以发现，的两个面是由对应的的两个面，沿轴正向平移lx得到的，对应的仿射变换矩阵为：

这里我们将面[1, 7]视为控制实体，将面[2, 8]视为周期实体，设置周期边界即先在[1, 7]面生成网格，再将生成的网格通过仿射变化（在我们这里是平移），复制到[2, 8]面上，对应的代码为：

translation_x = [1, 0, 0, lx,
                 0, 1, 0, 0,
                 0, 0, 1, 0,
                 0, 0, 0, 1]
gmsh.model.mesh.setPeriodic(2, [2, 8], [1, 7], translation_x)

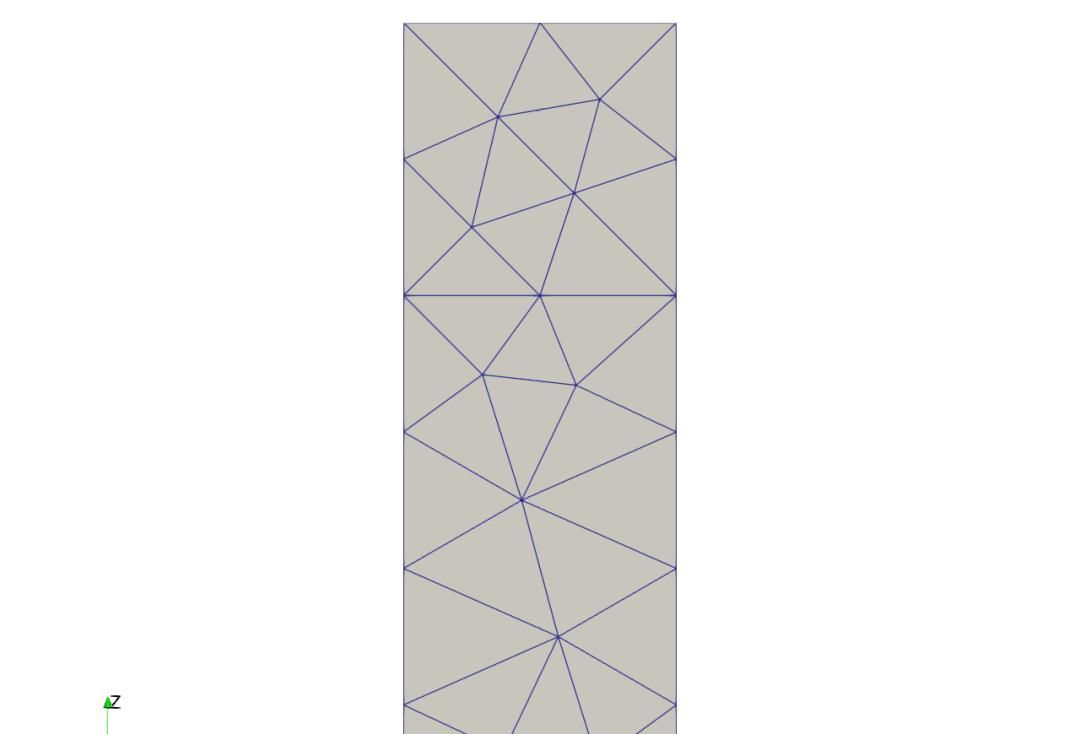
在这两个面上生成的网格如下：

注：在与视角看两者是对称的，实际则是沿着轴一一对应的。

更进一步的，还可以通过gmsh.model.mesh.getPeriodicNodes函数获取周期边界上对应的点标签：

tagMaster, nodeTags, nodeTagsMaster, _ = gmsh.model.mesh.getPeriodicNodes(2, 8)

输入周期边界的维数（这里为2），以及该周期边界的标签（面8），返回周期面8对应的控制面的标签（即面7），周期面8上的点标签列表，以及对应的控制面上的点标签列表。

完整代码如下：

import gmsh


# 初始化GMSH
gmsh.initialize()
gmsh.model.add("box")

# 定义box的尺寸
lx, ly, lz = 1.0, 1.0, 2.0

# 创建box
box1 = gmsh.model.occ.addBox(0, 0, 0, lx, ly, lz)
box2 = gmsh.model.occ.addBox(0, 0, lz, lx, ly, lz/2)
box = gmsh.model.occ.fragment([(3, box1)], [(3, box2)], removeObject=True)[0][0]

# 同步几何
gmsh.model.occ.synchronize()

# 设置网格密度，防止生成完全均匀的网格
gmsh.model.mesh.setSize(gmsh.model.getEntities(0), 0.5)
gmsh.model.mesh.setSize([(0, 6)], 0.1)

translation_x = [1, 0, 0, lx,
                 0, 1, 0, 0,
                 0, 0, 1, 0,
                 0, 0, 0, 1]
gmsh.model.mesh.setPeriodic(2, [2, 8], [1, 7], translation_x)

gmsh.model.mesh.generate(3)

tagMaster, nodeTags, nodeTagsMaster, _ = gmsh.model.mesh.getPeriodicNodes(2, 8)

# 结束GMSH
gmsh.finalize()