难度:A>C>B=D,开放度:D=B>A=C。原因如下:A题需多物理场建模(热弹性+结构力学),且需要结合仿真工具,专业门槛高。D题依赖生物数据的复杂特征提取和降噪,需处理高噪声混合信号。B题和C题以数学建模为主,但B题优化自由度更高,C题需处理电网拓扑约束。
同时,B题颜色空间转换需自定义损失函数,设计灵活性强,可结合多种优化方法。D题分析混合STR图谱的贡献者人数和比例,可尝试多种统计或机器学习模型。C题和A题约束条件明确,建模路径相对固定。
以下为ABCD题选题建议及初步分析:(要注意的是,本次选题建议会给出每道题目的题目分析、第一问建模过程和推荐算法,然后根据学生不同的专业,针对性给出选题建议)。
综合评价:
A题:专业性强,适合有工程建模经验的团队,但数据量少,需依赖仿真工具(如COMSOL)。
B题:开放度高,可结合机器学习和优化算法,适合数据驱动型团队。
C题:需处理电网拓扑约束,技术文档清晰但计算量大,适合系统建模能力强的团队。
D题:生物数据复杂且噪声高,需创新性算法设计,适合交叉学科团队。
2025年“深圳杯”数学建模挑战赛A题–芯片热弹性物理参数估计

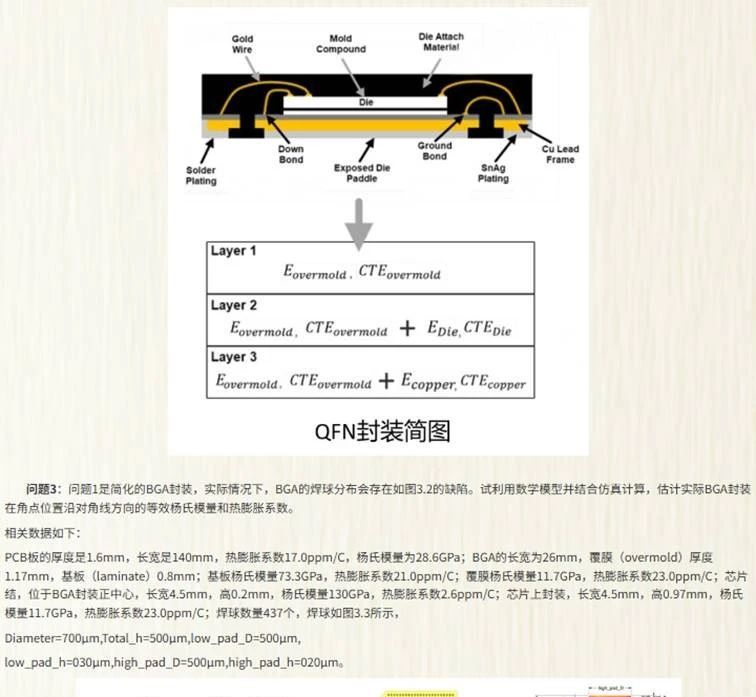
A题需估计非均质结构(BGA封装)角点处的等效杨氏模量和热膨胀系数,涉及多材料耦合、热弹性形变与疲劳失效。核心难点在于:
非均质结构建模:PCB、焊球、BGA的力学与热学参数差异显著,需建立等效模型;
多物理场耦合:温度循环下的热膨胀与弹性形变需同步分析;
局部参数敏感性:对角点位置的高风险区域进行参数聚焦。
建模过程为:

推荐算法:1 物理信息神经网络(PINN):将热弹性偏微分方程嵌入神经网络损失函数,直接求解等效参数;2 多尺度强化学习:通过深度Q网络(DQN)优化材料层间交互策略,提升等效参数估计效率;3 贝叶斯参数反演:结合马尔可夫链蒙特卡洛(MCMC)方法,量化参数不确定性。
大家可以使用这些可视化方法:
3D热力云图:使用ParaView或PyVista展示温度场与应力场的空间分布;
参数敏感性桑基图:通过Plotly动态展示各材料参数对等效模量的贡献路径;
多尺度仿真对比AR:利用增强现实工具(如Unity+Vuforia)叠加宏观与微观形变结果。
此题专业性强,适合有工程建模经验的团队,但数据量少,需依赖仿真工具(如COMSOL)。
问题1分析:
在问题一中,我们面对的是一个典型的异质结构等效物理参数估计问题。题目给出了PCB板、焊球与BGA组件的简化几何结构,要求估计其角点沿对角线方向的等效拉伸与弯曲杨氏模量以及等效热膨胀系数。由于这种结构具有周期性排列的焊球与层状结构,因此可以将其视为非均质复合材料系统,从材料力学的角度出发,通过等效材料理论对其力学与热学响应进行简化建模。在建模过程中,我们可以抽取穿过结构角点沿对角线方向的代表性路径,建立一维或二维的周期单胞模型,并运用串联与并联规则混合法来估计等效杨氏模量和热膨胀系数。串联模型适用于多种材料交替承受相同轴向应力的情形,而并联模型则适用于不同材料层共同变形的场景,通过材料在路径中所占比例进行加权计算。考虑到该结构在热疲劳下主要表现为角点失效,还可以进一步基于板壳理论,从弹性弯曲刚度公式出发,推导等效弯曲模量,构建更贴近物理现实的应力分析模型。此外,焊球数量与排列密度( m×m )对材料路径的影响不容忽视,可通过设置周期性边界或平均单胞的方式纳入模型。最终,形成一个反映宏观有效性能的简化数学表达式,为后续问题分析提供理论基础。
问题一:思路详解与建模过程
在问题一中,我们面对的是一个简化的BGA封装结构,它由PCB板、焊球阵列和BGA封装三种材料组成,要求估计封装对角线方向角点位置的等效拉伸杨氏模量、弯曲杨氏模量及等效热膨胀系数。这类问题属于非均质材料系统的热弹性参数等效建模问题。本质上,我们需要将复杂的微观多相结构“平均化”,构建一组可用于宏观热力分析的等效材料参数。




import numpy as np
import matplotlib.pyplot as plt
# 设置绘图风格
plt.style.use('seaborn-v0_8-darkgrid')
# ————————–
# 一、材料参数定义(单位:GPa, 1e-6 /°C)
# ————————–
E1 = 28.6 # PCB的杨氏模量
CTE1 = 17 # PCB的热膨胀系数
E2 = 50 # 焊球(如SnPb焊料)杨氏模量
CTE2 = 25 # 焊球热膨胀系数
E3 = 73.3 # BGA基板杨氏模量
CTE3 = 6.5 # BGA热膨胀系数
# ————————–
# 二、几何参数定义(单位:mm)
# ————————–
L = 26 # BGA封装边长
m = 21 # 焊球数量 m x m
d_ball = 0.5 # 每个焊球在对角方向等效长度
h1 = 1.6 # PCB厚度
h2 = 0.8 # 焊球高度
h3 = 1.17 # BGA厚度
# 计算对角线长度
L_diag = np.sqrt(2) * L
# 沿对角方向包含的焊球数和总长度
n_balls = m
l2 = n_balls * d_ball
# 剩余路径长度平分给PCB和BGA
l_remain = L_diag – l2
l1 = l3 = l_remain / 2
# 计算路径中三类材料的比例
alpha1 = l1 / L_diag
alpha2 = l2 / L_diag
alpha3 = l3 / L_diag
# ————————–
# 三、等效参数计算
# ————————–
# 等效拉伸杨氏模量(串联)
E_eq_tensile = 1 / (alpha1 / E1 + alpha2 / E2 + alpha3 / E3)
# 等效热膨胀系数(加权平均)
CTE_eq = alpha1 * CTE1 + alpha2 * CTE2 + alpha3 * CTE3
# 等效弯曲杨氏模量(简化层合模型)
I1 = h1 ** 3
I2 = h2 ** 3
I3 = h3 ** 3
E_eq_bending = (E1 * I1 + E2 * I2 + E3 * I3) / (I1 + I2 + I3)
# ————————–
# 四、结构分层图示(纵向层叠)
# ————————–
fig, ax = plt.subplots(figsize=(4, 6))
# 层级名称与厚度
layers = ['BGA', 'Solder Balls', 'PCB']
heights = [h3, h2, h1]
colors = ['#2ca02c', '#ff7f0e', '#1f77b4']
# 绘制分层结构
y_start = 0
for layer, height, color in zip(layers, heights, colors):
ax.barh(y=y_start + height / 2, width=40, height=height, left=0,
color=color, edgecolor='black')
ax.text(20, y_start + height / 2, f'{layer}
({height} mm)',
va='center', ha='center', fontsize=12, color='white', weight='bold')
y_start += height
# 图形参数调整
ax.set_xlim(0, 40)
ax.set_ylim(0, y_start + 1)
ax.set_title('Simplified Cross-Section of BGA Structure', fontsize=14)
ax.axis('off')
plt.tight_layout()
plt.show()
# ————————–
# 五、输出结果
# ————————–
print(f”等效拉伸杨氏模量 (E_eq_tensile): {E_eq_tensile:.2f} GPa”)
print(f”等效热膨胀系数 (CTE_eq): {CTE_eq:.2f} ×10⁻⁶ /°C”)
print(f”等效弯曲杨氏模量 (E_eq_bending): {E_eq_bending:.2f} GPa”)
2025年“深圳杯”数学建模挑战赛B题-LED显示屏颜色转换设计与校正
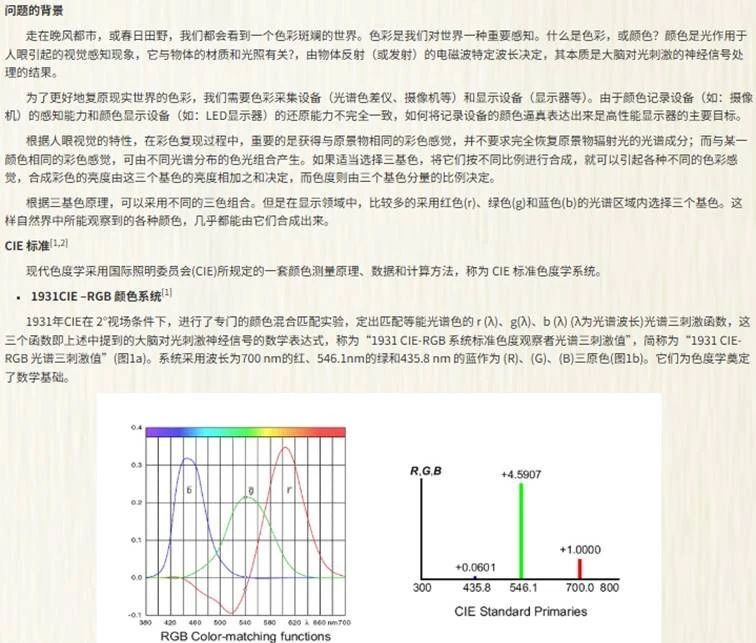
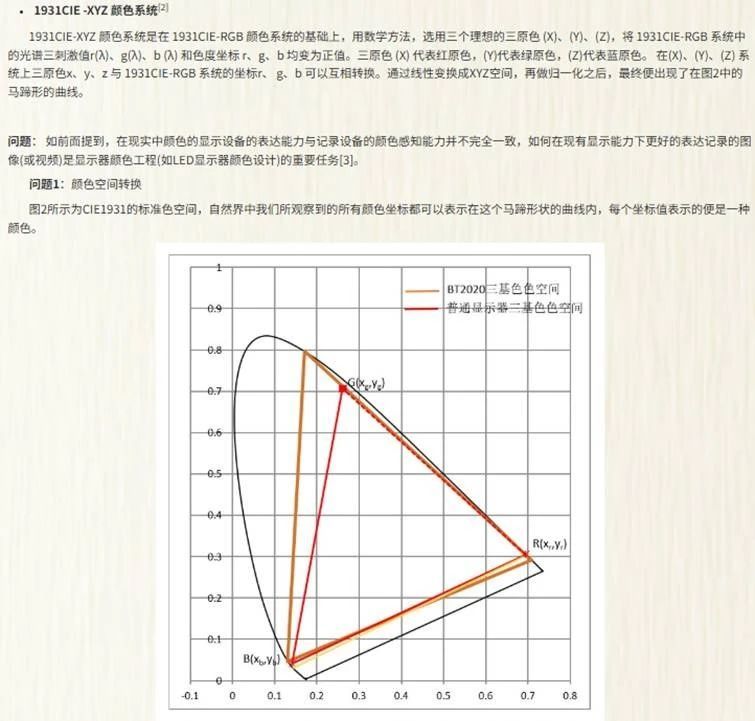
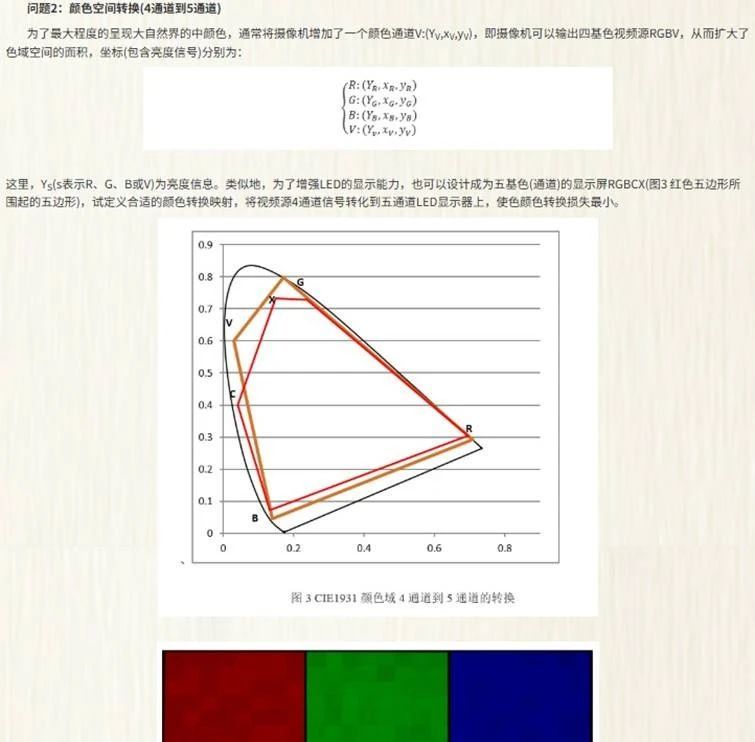


B题要求实现视频源色域(BT2020)到显示屏色域(RGB)的最小损失映射,核心难点是:
1 色域不匹配:目标色域超出显示设备能力,需压缩或映射;
2 多通道优化:四通道到五通道转换需高维空间映射;
3 亮度–色度分离:需保持亮度一致性同时优化色度差异。C君推荐的建模过程为:

推荐算法有:1 神经辐射场(NeRF)色域扩展:利用NeRF隐式表示学习色域外颜色,生成可显示近似色;2 Transformer跨域对齐:通过自注意力机制建立高维色域间语义对应关系;3 对抗生成网络(GAN):训练生成器将BT2020色域投影到RGB空间,判别器约束视觉逼真度。
可视化推荐:
动态色域马蹄图:使用Matplotlib或D3.js交互展示映射前后颜色分布;
色差热力图:基于PyQtGraph生成颜色差异的2D/3D密度图;
虚拟现实(VR)色域对比:通过Unity+SteamVR实现沉浸式色域差异观察。
推荐计算机等相关专业的同学进行选择 CV,开放度高,可结合机器学习和优化算法,适合数据驱动型团队。
2025年“深圳杯”数学建模挑战赛C题–分布式能源接入配电网的风险分析

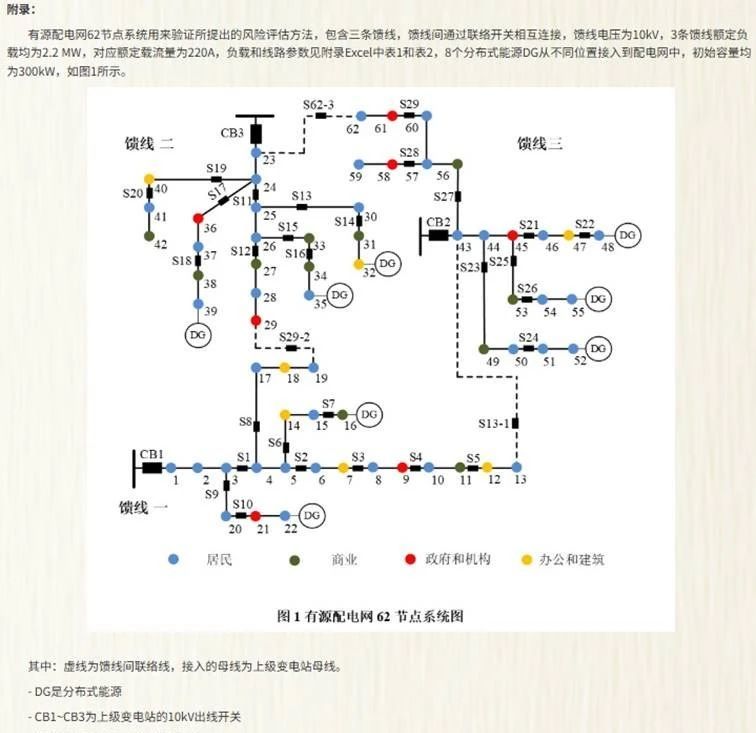
C题需建立失负荷与过负荷风险模型,核心在于1 电网拓扑约束:联络线转供需满足连通性且禁止反向送电;2 概率事件叠加:分布式电源(DG)波动导致多故障场景耦合;3经济-安全权衡:风险计算需结合停电损失与过载成本。

推荐使用1 图神经网络(GNN):学习电网拓扑特征,预测故障传播路径与风险;2 深度强化学习(DRL):训练智能体动态调整联络开关,优化负荷转移策略;3 不确定性量化(UQ):通过随机偏微分方程(SPDE)建模DG出力随机性。
推荐可视化:
动态拓扑风险热力图:使用Gephi或Cytoscape展示故障传播与风险分布;
3D风险演变曲面:利用Matplotlib或Three.js绘制容量-风险-时间的多维曲面;
交互式故障树:通过Plotly Dash构建可点击的故障路径分析面板。
这道题目的数据处理是重中之重大家需要认真去处理。需处理电网拓扑约束,技术文档清晰但计算量大,适合系统建模能力强的团队。
2025年“深圳杯”数学建模挑战赛D题–法医物证多人身份鉴定问题
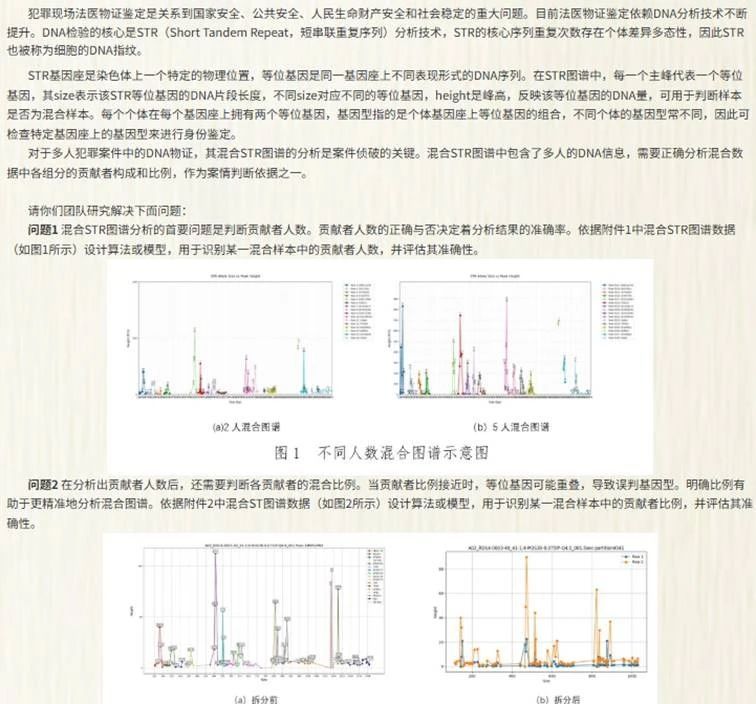
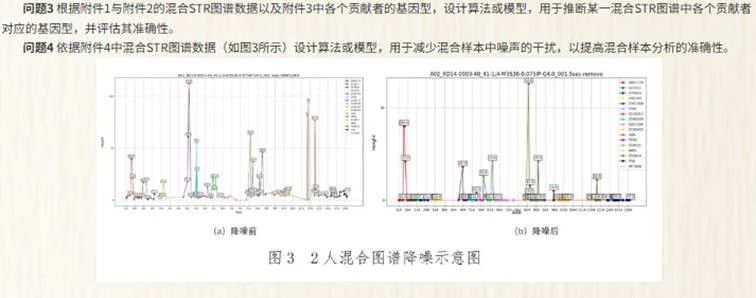
本题的核心任务是需从混合STR图谱推断贡献者人数、比例及基因型。
问题一的建模可以这样:

推荐算法:
深度嵌入聚类(DEC):联合学习特征表示与聚类中心,解决峰重叠问题;
变分自编码器(VAE):生成对抗噪声的STR谱,增强鲁棒性;
注意力机制Transformer:通过自注意力权重定位关键峰并分配贡献者。
可视化可以:

D题需生物信息学与信号处理结合,适合数据科学团队。难度适中,适合计算机、统计学、数学等相关专业的同学选择。
深圳杯&东三省数学建模联赛赛题浅析
赛题难度一图如下所示

A题:多个火箭残骸的准确定位
问题简述
u 单个残骸定位:确定用于精确测定单个空中火箭残骸音爆位置的最少监测设备数量,并计算指定数据中的残骸位置。
u 多个残骸定位:开发一个模型来分析和确定哪些震动波数据来自哪个残骸,并确定在空中有多个残骸同时发生音爆时的残骸位置和时间。
u 增强模型:在考虑监测设备记录时间可能存在的随机误差下,调整模型以更精确地确定多个残骸的位置和时间。
赛题浅析
此题要求根据多台设备接收到的音爆信号,准确定位火箭残骸的位置。基本原理是使用声波传播的时间差来推算距离,再利用这些距离来三角定位残骸的位置。
l 声速模型:设定声速为340 m/s,使用距离=速度×时间的公式计算残骸到每个监测点的距离。
l 三角测量:至少需要三个监测站来唯一确定一个空间点的位置。通过解算多个非线性方程组(基于测量的时间和已知的声速),确定残骸的具体位置。
数据处理:对收集的音爆抵达时间数据进行误差分析,考虑可能的误差来源(如仪器延迟、数据传输等)并进行校正。
模型优化:通过增加监测点数量、改善监测点布局或提升时间测量精度来优化定位精度。
B题:批量工件并行切割下料问题
问题简述
u 最大化板材利用率:为不同尺寸的板材设计一种切割排版方案,使得从中切割出的工件数量最多,且至少包含五种不同型号的工件。
u 最短切割时间:设计一个切割方案,使得使用最多五把刀具从给定板材中切割工件所需的时间最短。
u 多板材组合切割:给出一种策略,使用10把刀具从不同型号的板材中切割批量工件,并最小化总体切割时间,同时保持板材利用率高。
赛题浅析
几何模型与算法:
l 几何排版:开发一个算法来最大化板材利用率,同时满足工件之间和板边的最小间隙要求。这通常涉及到复杂的几何形状拟合和空间优化问题。
l 动态规划或启发式算法:利用动态规划或基于启发式的算法(如遗传算法、粒子群优化)来寻找最优切割路径。
多刀具协调:设计一个控制方案,以协调多个刀具的运动,确保切割过程的效率和准确性,同时考虑刀具间的最小距离约束。
模拟与验证:使用模拟软件(如MATLAB或专业CAD/CAM软件)模拟切割过程,评估切割方案的可行性和效率。
C题:编译器版本的识别问题
问题简述
u 特征提取:分析和识别不同版本GCC编译器编译同一C++程序的编译结果之间的区别。
u 构建判别函数:根据识别出的特征,创建一个函数来区分不同版本的编译器。
u 函数验证和泛化:验证判别函数的准确性,并调整其以提高对未知编译器版本的泛化能力。
赛题浅析
l 特征提取:分析由不同版本的编译器编译得到的二进制文件,提取能表征编译器特性的信息(如指令模式、优化级别、代码结构等)。
l 机器学习模型:
训练数据集:收集不同编译器版本和选项下的编译结果作为训练数据。
模型训练:使用分类算法(如决策树、支持向量机或神经网络)来学习并预测编译器版本。
l 模型验证与泛化:在多个编译器版本和选项下测试模型的准确性和泛化能力,分析模型的弱点并进行优化。
D题:音板的振动模态分析与参数识别
问题简述
u 振动模态分析:为不同材料和形状的音板建立振动数学模型,并比较其在2000 Hz内的振动频率和振型。
u 非均质音板模型:对具有非均匀厚度和弯曲度的音板进行振动模态分析,并预测其振型。
u 模态参数识别:使用实验数据来识别和调整音板的物理参数,以使模拟结果与实验数据尽可能一致。
赛题浅析
物理和数学模型:
l 振动模态理论:基于振动理论,建立描述音板振动的偏微分方程模型。考虑边界条件、材料属性(如杨氏模量、密度)对振动模态的影响。
l 频率和振型计算:使用数值方法(如有限元分析)来求解振动频率和振型。
参数反演:通过与实验数据对比,使用反问题技术来识别和校正音板的物理参数。
模拟与优化:对不同材料和设计的音板进行模拟,分析其振动特性,以指导实际的乐器设计和制造。






















暂无评论内容