❤七万字精华大合集！三年沉淀：从Python脚本到深度模型——构建数据科学全栈硬核知识体系。❤

文章摘要：

        在过去整整三年的时光里，我全身心地投入到学习与探索之中，将无数个日夜的钻研、思考与实践，凝结成了这篇博客。这篇总结犹如一座知识宝库，涵盖了Python、机器学习、深度学习等众多领域的精华内容。从20个硬核Python脚本，到机器学习中10种损失函数的全面梳理；从正则化算法、集成算法的总结，到聚类算法、SVM算法的深度剖析；从逻辑回归面试题的干货分享，到深度学习各算法优缺点及适用场景的探讨，再到Matplotlib的实用总结以及30个硬核数据集的呈现。每一个章节都倾注了我大量的心血，每一行文字都饱含着我对知识的执着与热爱。此刻，我怀着无比激动的心情，将这份三年磨一剑的成果呈现给大家，希望能为大家带来有价值的参考与启发。

目录

一、20个硬核Python脚本

二、机器学习中10种损失函数大梳理

三、机器学习正则化算法的总结

四、组合多个弱学习器达到性能跃升的硬核集成算法

五、逻辑回归面试题，机器学习干货、重点。

六、聚类算法的作用和怎么用

七、深度学习各算法的优缺点和适用场景

八、程序员最趁手的SVM算法

九、Matplotlib总结，任何项目都用得到

十、机器学习7大方面，30个硬核数据集

如果有感兴趣的模块请看看这个详细目录吧。

详细目录：

一、20个硬核Python脚本

1、Hello World

3、列表

4、字典

10、文件操作

11、日期和时间

12、随机数生成

13、正则表达式

14、Web请求

15、CSV文件处理

16、JSON处理

17、爬虫 – BeautifulSoup

18、多线程

二、机器学习中10种损失函数大梳理

1、均方误差

2、平均绝对误差

3、交叉熵损失

4、对数损失

5、多类别交叉熵损失

6、二分类交叉熵损失

7、余弦相似度损失

 8、希尔伯特-施密特口袋

9、Huber损失

10、 感知器损失

三、机器学习正则化算法的总结

1、L1 正则化（Lasso 正则化）

2、L2 正则化（岭正则化）

3、弹性网络正则化（Elastic Net 正则化）

4、Dropout 正则化（用于神经网络）

5、贝叶斯Ridge和Lasso回归

贝叶斯Ridge回归

贝叶斯Lasso回归

四、组合多个弱学习器达到性能跃升的硬核集成算法

1、Bagging（自举汇聚法）

2、Boosting（提升法）

3、Stacking（堆叠法）

4、Voting（投票法）

5、深度学习集成

五、逻辑回归面试题，机器学习干货、重点。

逻辑回归面试题 List

1、逻辑回归与线性回归有什么区别？

2、什么是逻辑回归的目标函数（损失函数）？常见的目标函数有哪些？

3、逻辑回归如何处理二分类问题？如何处理多分类问题？

4、什么是Sigmoid函数（逻辑函数）？它在逻辑回归中的作用是什么？

5、逻辑回归模型的参数是什么？如何训练这些参数？

6、什么是正则化在逻辑回归中的作用？L1和L2正则化有什么区别？

7、什么是特征工程，为什么它在逻辑回归中很重要？

8、逻辑回归的预测结果如何？怎样解释模型的系数（coefficient）？

9、什么是ROC曲线和AUC值？它们用来评估逻辑回归模型的哪些性能？

10、逻辑回归模型可能面临的问题有哪些？如何处理类不平衡问题？

11、什么是交叉验证，为什么在逻辑回归中使用它？

12、逻辑回归在实际应用中的一个例子是什么？描述一个应用场景，并如何使用逻辑回归来解决问题。

六、聚类算法的作用和怎么用

K均值聚类

原理介绍

公式表达

一个案例

层次聚类

原理介绍

公式表达

一个Python案例

密度聚类

原理介绍

关键概念

一个案例

谱聚类

原理介绍

一个Python案例

K-Means 聚类

层次聚类

DBSCAN

主成分分析

独立成分分析

高斯混合模型

七、深度学习各算法的优缺点和适用场景

前馈神经网络

1、梯度下降（Gradient Descent）

2、随机梯度下降（Stochastic Gradient Descent, SGD）

3、小批量梯度下降（Mini-batch Gradient Descent）

4、动量（Momentum）

5、AdaGrad、RMSprop、Adam等自适应学习率算法

卷积神经网络

1、LeNet-5

2、AlexNet

3、VGGNet

4、GoogLeNet/Inception

5、ResNet (Residual Networks)

1、SGD（随机梯度下降）

2、Adam（自适应矩估计）

3、RMSprop

4、Batch Normalization

循环神经网络

1、Vanilla RNN

2、LSTM（长短时记忆）

3、GRU（门控循环单元）

4、Bidirectional RNN

1、Teacher Forcing

2、Attention Mechanism

3、Seq2Seq（Sequence to Sequence）

4、Dropout

5、Batch Normalization

长短时记忆网络

1、标准LSTM

2、双向LSTM（Bidirectional LSTM）

3、多层LSTM（Multilayer LSTM）

4、GRU（Gated Recurrent Unit）

5、Peephole LSTM

6、LSTM变种（如Stacked LSTM、Attention LSTM等）

生成对抗网络

1、原始GAN

2、Deep Convolutional GAN（DCGAN）

3、Conditional GAN（cGAN）

4、Wasserstein GAN（WGAN）

5、CycleGAN

6、Progressive GAN

7、Self-Attention GAN（SAGAN）

八、程序员最趁手的SVM算法

1线性支持向量机

2非线性支持向量机

3多类别支持向量机

4核函数支持向量机

5稀疏支持向量机

九、Matplotlib总结，任何项目都用得到

1、绘制基本图形

2、定制化图形

3、支持多个坐标轴

4、3D绘图

5、动态交互绘图

6、绘制地图

7、绘制统计图表

十、机器学习7大方面，30个硬核数据集

回归问题

分类问题

图像分类

文本情感分析

自然语言处理

自动驾驶

金融类

最后

---

一、20个硬核Python脚本

1、Hello World

print("Hello, World!")

官方文档: https://docs.python.org/3/

2、变量和数据类型

name = "Alice"
age = 30
height = 175.5
is_student = True

官方文档: https://docs.python.org/3/tutorial/introduction.html#numbers

3、列表

fruits = ["apple", "banana", "cherry"]
fruits.append("date")
print(fruits)

官方文档: https://docs.python.org/3/tutorial/introduction.html#lists

4、字典

person = {"name": "Alice", "age": 30, "city": "New York"}
print(person["name"])

5、循环

for i in range(1, 6):
    print(i)

官方文档: https://docs.python.org/3/tutorial/introduction.html#first-steps-towards-programming

6、条件语句

x = 5
if x > 10:
    print("x is greater than 10")
else:
    print("x is not greater than 10")

官方文档: https://docs.python.org/3/tutorial/controlflow.html

7、函数

def greet(name):
    return f"Hello, {name}!"

message = greet("Alice")
print(message)

官方文档: https://docs.python.org/3/tutorial/controlflow.html#defining-functions

8、模块导入

import math

print(math.sqrt(16))

官方文档: https://docs.python.org/3/tutorial/modules.html

9、异常处理

try:
    result = 10 / 0
except ZeroDivisionError:
    print("Division by zero is not allowed.")

官方文档: https://docs.python.org/3/tutorial/errors.html

10、文件操作

with open("example.txt", "w") as file:
    file.write("Hello, File!")

with open("example.txt", "r") as file:
    content = file.read()
    print(content)

官方文档: https://docs.python.org/3/tutorial/inputoutput.html

11、日期和时间

from datetime import datetime

now = datetime.now()
print(now)

官方文档: https://docs.python.org/3/library/datetime.html

12、随机数生成

import random

random_number = random.randint(1, 100)
print(random_number)

13、正则表达式

import re

text = "Hello, 12345"
pattern = r'd+'
match = re.search(pattern, text)
if match:
    print(match.group())

官方文档: https://docs.python.org/3/library/re.html

14、Web请求

import requests

response = requests.get("https://www.example.com")
print(response.text)

官方文档: https://docs.python-requests.org/en/master/

15、CSV文件处理

import csv

with open("data.csv", "w", newline="") as file:
    writer = csv.writer(file)
    writer.writerow(["Name", "Age"])
    writer.writerow(["Alice", 25])

with open("data.csv", "r") as file:
    reader = csv.reader(file)
    for row in reader:
        print(row)

官方文档: https://docs.python.org/3/library/csv.html

16、JSON处理

import json

data = {"name": "Bob", "age": 35}
json_data = json.dumps(data)
print(json_data)

官方文档: https://docs.python.org/3/library/json.html

17、爬虫 – BeautifulSoup

from bs4 import BeautifulSoup
import requests

url = "https://www.example.com"
response = requests.get(url)
soup = BeautifulSoup(response.text, "html.parser")
print(soup.title.text)

官方文档: https://www.crummy.com/software/BeautifulSoup/bs4/doc/

18、多线程

import threading

def print_numbers():
    for i in range(1, 6):
        print(f"Number: {i}")

def print_letters():
    for letter in "abcde":
        print(f"Letter: {letter}")

thread1 = threading.Thread(target=print_numbers)
thread2 = threading.Thread(target=print_letters)

thread1.start()
thread2.start()

官方文档: https://docs.python.org/3/library/threading.html

19、数据爬取 – Selenium

from selenium import webdriver

driver = webdriver.Chrome()
driver.get("https://www.example.com")

官方文档: https://www.selenium.dev/documentation/en/

20、REST API – Flask

from flask import Flask, jsonify

app = Flask(__name)

@app.route('/api', methods=['GET'])
def get_data():
    data = {'message': 'Hello, API!'}
    return jsonify(data)

if __name__ == '__main__':
    app.run()

官方文档: https://flask.palletsprojects.com/en/2.1.x/

二、机器学习中10种损失函数大梳理

1、均方误差

2、平均绝对误差

3、交叉熵损失

4、对数损失

5、多类别交叉熵损失

6、二分类交叉熵损失

7、余弦相似度损失

 8、希尔伯特-施密特口袋

9、Huber损失

10、 感知器损失

---

 损失函数（Loss Function）是在机器学习和深度学习中用来衡量模型预测值与真实标签之间差异的函数。不同的任务和模型可能需要不同的损失函数。

今天就聊聊下面常见的损失函数，关于原理、使用场景，并且给出完整的代码：

均方误差

平均绝对误差

交叉熵损失

对数损失

多类别交叉熵损失

二分类交叉熵损失

余弦相似度损失

希尔伯特-施密特口袋

Huber损失

感知器损失

ok，咱们一起来学习一下~

1、均方误差

均方误差是一种常用的损失函数，通常用于衡量回归模型预测结果与真实值之间的差异程度。

均方误差是通过计算预测值与真实值之间差异的平方和来衡量模型的性能。它对于较大的差异给予更高的权重，因为平方操作会放大较大的差异。均方误差的数值越小，表示模型预测的结果与真实值越接近。

均方误差的公式：

import numpy as np
import matplotlib.pyplot as plt

# 真实值和预测值
y_true = np.array([1, 2, 3, 4, 5])
y_pred = np.array([1.2, 2.5, 3.7, 4.1, 5.3])

# 计算均方误差
mse = np.mean((y_true - y_pred) ** 2)
print("MSE:", mse)

# 绘制真实值和预测值的散点图
plt.scatter(y_true, y_pred)
plt.plot([min(y_true), max(y_true)], [min(y_true), max(y_true)], 'k--', lw=2)  # 绘制直线y=x
plt.xlabel('True Values')
plt.ylabel('Predicted Values')
plt.title('Scatter plot of True vs Predicted Values')
plt.show()

运行这段代码将计算出均方误差，并绘制出一个散点图，其中x轴表示真实值，y轴表示预测值。通过与直线y=x进行比较，可以看到预测值与真实值之间的差异程度。较接近直线的点表示预测结果较准确。

2、平均绝对误差

平均绝对误差（Mean Absolute Error，MAE）是一种用于衡量预测模型性能的损失函数，通常用于回归问题。它衡量了模型的预测值与实际观测值之间的平均绝对差异。MAE 的值越小，表示模型的预测越准确。

MAE 的原理非常简单，它是所有绝对误差的平均值。绝对误差是指每个观测值的预测值与实际值之间的差的绝对值。

平均绝对误差的计算公式：

 

import numpy as np
import matplotlib.pyplot as plt

# 生成随机数据
np.random.seed(0)
n = 50
X = np.linspace(0, 10, n)
y_true = 2 * X + 1 + np.random.normal(0, 1, n)  # 真实的目标值，包含随机噪音
y_pred = 2 * X + 1.5  # 模拟的预测值

# 计算MAE
mae = np.mean(np.abs(y_true - y_pred))

# 绘制数据点和预测线
plt.scatter(X, y_true, label='Actual', color='b')
plt.plot(X, y_pred, label='Predicted', color='r')
plt.title(f'MAE = {mae:.2f}')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.show()

代码中，首先生成了一些随机的数据点，然后计算了 MAE，并用散点图和预测线将数据可视化出来。MAE 的值会显示在图的标题中。

通过这个示例，你可以直观地了解 MAE 的计算和它如何衡量模型的性能。MAE 越小，预测值越接近实际值。

3、交叉熵损失

交叉熵损失（Cross-Entropy Loss）是机器学习中常用的一种损失函数，主要应用于分类问题。它用于衡量模型预测结果与实际标签之间的差异。

交叉熵损失基于信息论中的交叉熵概念，用于度量两个概率分布之间的相似性。在分类问题中，我们将实际标签表示为一个one-hot向量，即只有一个元素为1，其余元素为0；而模型的预测结果通常是一个概率分布。交叉熵损失通过计算实际标签和模型预测结果之间的交叉熵来评估模型的性能。

对于多分类问题，交叉熵损失可以表示为：

其中，为实际标签中第个类别的概率（one-hot编码），为模型预测的第个类别的概率。

一个Python案例

以下是一个多分类问题的例子，使用交叉熵损失进行模型训练：

import numpy as np
import matplotlib.pyplot as plt

def cross_entropy_loss(y_true, p_pred):
    epsilon = 1e-10  # 添加一个小的常数以避免log(0)计算错误
    return -np.sum(y_true * np.log(p_pred + epsilon), axis=1)

# 模拟数据
num_samples = 1000
num_classes = 5

np.random.seed(42)
y_true = np.eye(num_classes)[np.random.choice(num_classes, num_samples)]  # 生成随机的one-hot标签
p_pred = np.random.rand(num_samples, num_classes)  # 模型预测的概率

loss = cross_entropy_loss(y_true, p_pred)

# 计算平均损失
average_loss = np.mean(loss)

# 绘制损失函数图形
plt.plot(range(num_samples), loss, 'bo', markersize=2)
plt.xlabel('Sample')
plt.ylabel('Cross-Entropy Loss')
plt.title('Cross-Entropy Loss for each Sample')
plt.axhline(average_loss, color='r', linestyle='--', label='Average Loss')
plt.legend()
plt.show()

print(f'Average Loss: {average_loss}')

代码中，首先定义了一个cross_entropy_loss函数来计算交叉熵损失。然后，我们模拟了一个多分类问题的数据集，其中包含1000个样本和5个类别。接下来，使用该函数计算模型预测结果和实际标签之间的交叉熵损失，并计算平均损失。最后，使用Matplotlib库绘制了每个样本的交叉熵损失，并在图形中用一条红色虚线表示平均损失。

在实际应用中，通常会结合优化算法（如梯度下降）来最小化交叉熵损失，并优化模型的预测性能。

4、对数损失

对数损失（Log Loss），也称为二分类交叉熵损失，是机器学习中常用的一种损失函数之一，主要适用于二分类问题。它用于衡量模型预测结果与实际标签之间的差异。

对数损失基于信息论中的交叉熵概念，用于度量两个概率分布之间的相似性。在二分类问题中，通常使用0和1表示实际标签，而模型的预测结果是一个介于0和1之间的概率值。对数损失通过计算实际标签和模型预测结果的交叉熵来评估模型的性能。

对数损失可以表示为：

import numpy as np
import matplotlib.pyplot as plt

def log_loss(y_true, p_pred):
    epsilon = 1e-10  # 添加一个小的常数以避免log(0)计算错误
    return - (y_true * np.log(p_pred + epsilon) + (1 - y_true) * np.log(1 - p_pred + epsilon))

# 模拟数据
num_samples = 1000

np.random.seed(42)
y_true = np.random.randint(2, size=num_samples)  # 随机生成0和1的实际标签
p_pred = np.random.rand(num_samples)  # 模型预测的概率

loss = log_loss(y_true, p_pred)

# 计算平均损失
average_loss = np.mean(loss)

# 绘制损失函数图形
plt.plot(range(num_samples), loss, 'bo', markersize=2)
plt.xlabel('Sample')
plt.ylabel('Log Loss')
plt.title('Log Loss for each Sample')
plt.axhline(average_loss, color='r', linestyle='--', label='Average Loss')
plt.legend()
plt.show()

print(f'Average Loss: {average_loss}')

5、多类别交叉熵损失

多类别交叉熵损失是机器学习中常用的一种损失函数，用于衡量模型输出与真实标签之间的差异。它适用于多分类问题，其中每个样本有一个唯一的类别标签。

该损失函数通过计算模型预测的概率分布与真实标签的概率分布之间的交叉熵来度量它们之间的差异。交叉熵是一个非负的值，当且仅当预测的概率分布与真实标签完全匹配时为零。

假设我们有一个样本，其真实标签表示为一个one-hot向量（只有一个元素为1，其他元素为0）。假设模型的输出是一个概率分布向量，表示模型对每个类别的预测概率。则多类别交叉熵损失的公式如下：

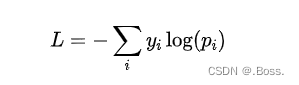
其中， 是真实标签向量中第个元素的值（0或1）， 是模型输出的概率分布向量中第个元素的值。

一个Python案例

下面是一个使用Python实现的多类别交叉熵损失的案例。

import numpy as np
import matplotlib.pyplot as plt

def categorical_cross_entropy(y_true, y_pred):
    # 避免出现概率为0的情况，加上一个小的偏移量
    epsilon = 1e-7
    # 计算交叉熵损失
    loss = -np.sum(y_true * np.log(y_pred + epsilon))
    return loss

# 生成随机的真实标签和预测概率分布
np.random.seed(42)
num_classes = 4
num_samples = 1000
y_true = np.random.randint(num_classes, size=num_samples)
y_pred = np.random.rand(num_samples, num_classes)

# 将真实标签转换为one-hot向量
y_true_one_hot = np.eye(num_classes)[y_true]

# 计算多类别交叉熵损失
loss = categorical_cross_entropy(y_true_one_hot, y_pred)
print("Loss:", loss)

# 绘制损失函数的图形
x = np.arange(0.01, 1.0, 0.01)
y = -np.log(x)
plt.plot(x, y)
plt.xlabel("Predicted Probability")
plt.ylabel("Loss")
plt.title("Categorical Cross-Entropy Loss")
plt.show()

在这个案例中，我们首先生成了随机的真实标签和预测概率分布。然后将真实标签转换为one-hot向量，以便与预测概率分布进行计算。

最后，使用categorical_cross_entropy函数计算多类别交叉熵损失，并输出结果。

同时，我们将绘制损失函数图形，其中横轴表示预测的概率，纵轴表示对应的损失值。

6、二分类交叉熵损失

二分类交叉熵损失是机器学习中常用的一种损失函数，适用于二分类问题，其中每个样本只有两个可能的类别。

该损失函数通过计算模型输出的概率与真实标签之间的交叉熵来衡量它们之间的差异。交叉熵是一个非负的值，当且仅当预测的概率与真实标签一致时为零。

假设我们有一个样本，其真实标签表示为0或1。假设模型的输出是一个[0, 1]范围内的概率，表示模型对类别1的预测概率。则二分类交叉熵损失的公式如下：

 

import numpy as np
import matplotlib.pyplot as plt

def binary_cross_entropy(y_true, y_pred):
    # 避免出现概率为0或1的情况，加上一个小的偏移量
    epsilon = 1e-7
    # 计算交叉熵损失
    loss = -y_true * np.log(y_pred + epsilon) - (1 - y_true) * np.log(1 - y_pred + epsilon)
    return loss

# 生成随机的真实标签和预测概率
np.random.seed(42)
num_samples = 1000
y_true = np.random.randint(2, size=num_samples)
y_pred = np.random.rand(num_samples)

# 计算二分类交叉熵损失
loss = binary_cross_entropy(y_true, y_pred)
print("Loss:", loss[:10])  # 打印前10个样本的损失值

# 绘制损失函数的图形
x = np.linspace(0.01, 0.99, 100)
y = -np.log(x) - np.log(1 - x)
plt.plot(x, y)
plt.xlabel("Predicted Probability")
plt.ylabel("Loss")
plt.title("Binary Cross-Entropy Loss")
plt.show()

在这个案例中，我们首先生成了随机的真实标签和预测概率。然后使用binary_cross_entropy函数计算二分类交叉熵损失，并输出结果。同时，我们将绘制损失函数图形，其中横轴表示预测的概率，纵轴表示对应的损失值。

7、余弦相似度损失

余弦相似度损失是一种常用的机器学习损失函数，用于衡量向量之间的相似性。它基于向量的内积和范数来计算相似度，并将其转化为一个损失值。

余弦相似度损失基于余弦相似度的概念。余弦相似度是两个向量之间的夹角的余弦值，范围在-1到1之间。当夹角为0度时，余弦相似度为1，表示两个向量完全相同；当夹角为90度时，余弦相似度为0，表示两个向量无关；当夹角为180度时，余弦相似度为-1，表示两个向量完全相反。

公式表达：假设有两个向量A和B，余弦相似度可以通过以下公式计算：

import numpy as np
import matplotlib.pyplot as plt

# 生成随机数据
np.random.seed(0)
x = np.linspace(-10, 10, 100)
y_true = np.sin(x) + np.random.normal(0, 0.1, size=(100,))

# 定义交叉熵损失函数
def cross_entropy_loss(y_true, y_pred):
    epsilon = 1e-7  # 避免log(0)的情况
    loss = -np.mean(y_true * np.log(y_pred + epsilon) + (1 - y_true) * np.log(1 - y_pred + epsilon))
    return loss

# 假设预测值为正弦函数
y_pred = np.sin(x)

# 计算交叉熵损失
loss = cross_entropy_loss(y_true, y_pred)

# 绘制图形
plt.plot(x, y_true, label='True')
plt.plot(x, y_pred, label='Predicted')
plt.title(f'Cross Entropy Loss: {loss:.4f}')
plt.legend()
plt.show()

上述代码生成了一个包含随机噪声的正弦函数作为真实值，并假设预测值也是正弦函数。通过交叉熵损失函数计算出损失值，并用图形表示出真实值和预测值。注意，这里的交叉熵损失函数假设了二分类问题，因此y_true和y_pred都是取值在0到1之间的概率值。

 8、希尔伯特-施密特口袋

希尔伯特-施密特口袋（Hinge-Schmidt Pocket）是一种用于支持向量机训练的损失函数。它是一种改进的希尔伯特-施密特损失函数，旨在更好地处理线性可分和线性不可分问题。

在解释希尔伯特-施密特口袋之前，我们先来了解一下标准的希尔伯特-施密特损失函数。

希尔伯特-施密特损失函数

希尔伯特-施密特损失函数是SVM中常用的损失函数之一，用于二分类问题的训练。其主要思想是要找到一个超平面，将两个类别的数据分开，并最大化这个超平面与最近的数据点（支持向量）之间的间隔。

损失函数的公式： 

下面我们将演示如何使用Python和Scikit-Learn来执行一个简单的二分类问题，使用交叉熵损失函数来训练一个逻辑回归模型，并绘制决策边界的图形。

首先，我们需要导入必要的库和生成一些模拟数据。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression

# 生成模拟数据
X, y = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_classes=2, random_state=42)

# 创建逻辑回归模型
model = LogisticRegression()

# 训练模型
model.fit(X, y)

# 用于绘制决策边界的辅助函数
def plot_decision_boundary(X, y, model):
    xx, yy = np.meshgrid(np.linspace(X[:, 0].min() - 1, X[:, 0].max() + 1, 100),
                         np.linspace(X[:, 1].min() - 1, X[:, 1].max() + 1, 100))
    Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    plt.contourf(xx, yy, Z, alpha=0.8)
    plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k')
    plt.xlabel('Feature 1')
    plt.ylabel('Feature 2')
    plt.show()

# 绘制决策边界
plot_decision_boundary(X, y, model)

这段代码生成了一个二维的模拟数据集，使用Scikit-Learn的逻辑回归模型进行训练，并绘制了决策边界的图形。决策边界将两个类别的数据分开。

交叉熵损失在逻辑回归模型中是默认的损失函数，它在模型训练过程中最小化损失来找到最佳的参数（权重和偏置）。

9、Huber损失

Huber损失是一种用于回归问题的损失函数，它对异常值不敏感，相比于均方误差（MSE），它对异常值的惩罚较小。Huber损失的主要思想是在距离真实值较近的情况下采用均方误差，而在距离较远的情况下采用绝对误差，这种权衡可以有效减少异常值的影响。

Huber损失的公式：

import numpy as np
import matplotlib.pyplot as plt

# 定义Huber损失函数
def huber_loss(y_true, y_pred, delta):
    error = np.abs(y_true - y_pred)
    if error <= delta:
        return 0.5 * error**2
    else:
        return delta * error - 0.5 * delta**2

# 生成一些样本数据
np.random.seed(0)
X = np.linspace(0, 10, 100)
y_true = 2 * X + 1 + np.random.normal(0, 1, 100)

# 定义模型预测值
y_pred = 2 * X + 1

# 计算不同delta值下的损失
deltas = [1.0, 2.0, 5.0]
losses = []

for delta in deltas:
    loss = [huber_loss(y_true[i], y_pred[i], delta) for i in range(len(X))]
    losses.append(loss)

# 绘制损失曲线
plt.figure(figsize=(10, 6))
for i, delta in enumerate(deltas):
    plt.plot(X, losses[i], label=f'Huber Loss (delta={delta})')

plt.xlabel('X')
plt.ylabel('Loss')
plt.title('Huber Loss for Different Delta Values')
plt.legend()
plt.grid(True)
plt.show()

代码中，首先定义了Huber损失函数，然后生成了一些样本数据，包括真实的目标值和模型的预测值。接下来，我们计算了不同delta值下的损失，并绘制了损失曲线。从图中可以清晰地看出，随着delta值的增大，Huber损失在异常值处的惩罚逐渐减小，这是Huber损失相对于均方误差的一个重要特点。

以上示例说明了Huber损失如何在不同情况下平衡均方误差和绝对误差，以减少异常值对损失的影响。

10、 感知器损失

感知器损失函数，也称为0-1损失函数，是一种用于二元分类任务的损失函数。

它的原理非常简单：它将分类问题的输出与真实标签进行比较，如果预测正确则损失为0，否则损失为1。

感知器损失函数的公式：

import numpy as np
import matplotlib.pyplot as plt

# Generate random binary classification dataset
np.random.seed(0)
X = np.random.rand(100, 2)  # 100 samples with 2 features each
y = (X[:, 0] + X[:, 1] > 1).astype(int)  # Labels: 1 if sum of features > 1, else 0

# Assume our model always predicts 1 for demonstration
y_pred = np.ones_like(y)

# Calculate perceptron loss
loss = np.mean(np.abs(y - y_pred))

# Print the loss value
print(f"Perceptron Loss: {loss}")

# Plot data points and decision boundary
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired)
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.title("Binary Classification Dataset and Decision Boundary")

# Plot the decision boundary (a simple straight line here)
x_line = np.linspace(0, 1.2, 100)
y_line = 1 - x_line
plt.plot(x_line, y_line, 'k--', label="Decision Boundary")
plt.legend()
plt.show()

当然，在特定的场景和条件下，很大情况下需要自定义损失函数~

三、机器学习正则化算法的总结

 正则化是一种用于降低机器学习模型过拟合风险的技术。当模型过度拟合训练数据时，它会在新样本上表现不佳。所以为了解决这个问题，我们必须要引入正则化算法。

正则化通过在模型的损失函数中添加一个正则项（惩罚项）来实现。这个正则项通常基于模型参数的大小，以限制模型参数的数量或幅度。主要有两种常见的正则化算法：L1正则化和L2正则化。

L1正则化（Lasso）：L1正则化添加了模型参数的绝对值之和作为正则项。它倾向于使一些参数变为零，从而达到特征选择的效果。所以，L1正则化可以用于自动选择最重要的特征，并减少模型复杂度。

L2正则化（Ridge）：L2正则化添加了模型参数的平方和作为正则项。它倾向于使所有参数都较小，但没有明确地将某些参数设置为零。L2正则化对异常值更加鲁棒，并且可以减少模型的过度依赖单个特征的情况。

正则化通过控制模型参数的大小来限制模型的复杂度，从而避免过拟合。在损失函数中引入正则项后，模型的优化目标变为最小化损失函数和正则项之和。

今天要探究的是这7各部分，大家请看~

L1 正则化

L2 正则化

弹性网络正则化

Dropout 正则化

贝叶斯Ridge和Lasso回归

早停法

数据增强

1、L1 正则化（Lasso 正则化）

L1正则化（也称为Lasso正则化）是一种用于控制机器学习模型复杂度的技术。

通过向损失函数添加L1范数项来实现正则化，鼓励模型产生稀疏权重，即将一些特征的权重调整为0。

公式：

L1正则化在优化过程中有两个关键特点：

1、由于正则化项中包含绝对值操作，导致损失函数不可导。因此，在求解最小化损失函数时，需要使用其他方法（如坐标下降、梯度下降等）。

2、正则化项的存在促使部分特征的权重变为0，从而实现特征选择和模型简化。

咱们看一个简单案例，使用了sklearn库中的Lasso类来实现L1正则化的模型：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Lasso

# 生成示例数据
np.random.seed(42)
X = np.linspace(-5, 5, num=100).reshape(-1, 1)
y = 2 * X + np.random.normal(0, 1, size=(100, 1))

# 创建Lasso模型对象
lasso = Lasso(alpha=0.1)  # 设置alpha参数，控制正则化强度

# 拟合数据
lasso.fit(X, y)

# 绘制优化复杂图形
fig, ax = plt.subplots()
ax.scatter(X, y, color="blue", label="Data")
ax.plot(X, lasso.predict(X), color="red", linewidth=2, label="L1 Regularization")

# 在图中绘制L1正则化项的等高线
beta_0 = np.linspace(-10, 10, 100)
beta_1 = np.linspace(-10, 10, 100)
B0, B1 = np.meshgrid(beta_0, beta_1)
Z = np.zeros_like(B0)
for i in range(len(beta_0)):
    for j in range(len(beta_1)):
        lasso.coef_ = np.array([B0[i,j], B1[i,j]])
        Z[i,j] = np.sum(np.abs(lasso.coef_))
ax.contour(B0, B1, Z, levels=20, colors="black", alpha=0.5)

ax.set_xlabel("X")
ax.set_ylabel("y")
ax.set_title("L1 Regularization with Contour Plot")
ax.legend()
plt.show()

除了绘制原始数据点和经过L1正则化的拟合线外，我们还使用等高线图形展示了L1正则化项。通过等高线图，可以更加直观地看到正则化项对权重的影响，以及如何促使模型产生稀疏权重。

2、L2 正则化（岭正则化）

L2正则化（也称为岭正则化）是一种用于控制机器学习模型复杂度的技术。

它通过向损失函数添加L2范数项来实现正则化，鼓励模型产生平滑权重，即将特征的权重调整为较小的值。

公式：

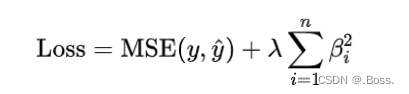
L2正则化在优化过程中的2个关键特点：

1、正则化项中包含平方操作，使得损失函数可导。因此，在求解最小化损失函数时，可以使用常见的梯度下降等优化算法。

2、正则化项的存在使得特征权重趋向于较小的值，从而避免了过拟合问题。

先看一个案例，使用sklearn库中的Ridge类来实现L2正则化的模型：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge

# 生成示例数据
np.random.seed(42)
X = np.linspace(-5, 5, num=100).reshape(-1, 1)
y = 2 * X + np.random.normal(0, 1, size=(100, 1))

# 创建Ridge模型对象
ridge = Ridge(alpha=0.1)  # 设置alpha参数，控制正则化强度

# 拟合数据
ridge.fit(X, y)

# 绘制优化复杂图形
fig, ax = plt.subplots()
ax.scatter(X, y, color="blue", label="Data")
ax.plot(X, ridge.predict(X), color="red", linewidth=2, label="L2 Regularization")

# 在图中绘制L2正则化项的等高线
beta_0 = np.linspace(-10, 10, 100)
beta_1 = np.linspace(-10, 10, 100)
B0, B1 = np.meshgrid(beta_0, beta_1)
Z = np.zeros_like(B0)
for i in range(len(beta_0)):
    for j in range(len(beta_1)):
        ridge.coef_ = np.array([B0[i,j], B1[i,j]])
        Z[i,j] = np.sum(ridge.coef_ ** 2)
ax.contour(B0, B1, Z, levels=20, colors="black", alpha=0.5)

ax.set_xlabel("X")
ax.set_ylabel("y")
ax.set_title("L2 Regularization with Contour Plot")
ax.legend()
plt.show()

除了绘制原始数据点和经过L2正则化的拟合线外，我们还使用等高线图形展示了L2正则化项。通过等高线图，可以更加直观地看到正则化项对权重的影响，以及如何促使模型产生平滑权重。

3、弹性网络正则化（Elastic Net 正则化）

弹性网络正则化是一种用于线性回归模型的正则化方法，结合了L1和L2正则化的特点。

可以在具有大量特征的数据集上处理多重共线性问题，并选择相关特征。

弹性网络正则化通过加权L1范数和L2范数来控制正则化项的大小。L1范数在某些情况下会产生稀疏解（即部分系数为零），而L2范数鼓励系数的平滑性。

因此，弹性网络正则化可以综合利用L1和L2正则化的优势。

弹性网络正则化的损失函数可以表示为：

下面是使用Python的scikit-learn库来拟合弹性网络回归模型：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import ElasticNet

# 生成一些样本数据
np.random.seed(42)
n_samples = 100
X = np.linspace(-3, 3, n_samples)
y = 0.5 * X + np.random.normal(scale=0.5, size=n_samples)

# 创建并拟合弹性网络模型
enet = ElasticNet(alpha=0.5, l1_ratio=0.7)
enet.fit(X.reshape(-1, 1), y)

# 绘制原始数据和拟合曲线
plt.scatter(X, y, color='b', label='Original data')
plt.plot(X, enet.predict(X.reshape(-1, 1)), color='r', linewidth=2, label='Elastic Net')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title('Elastic Net Regression')
plt.show()

代码中生成了一些具有噪声的样本数据，并使用弹性网络模型进行拟合。

通过绘制原始数据和拟合曲线，可以更好地理解弹性网络正则化在回归问题中的应用。

案例中只是一个简单的示例，实际使用时需要调整参数和改进模型以适应具体问题。

4、Dropout 正则化（用于神经网络）

Dropout 正则化是一种用于神经网络的正则化方法。

通过在训练过程中随机将一部分神经元的输出设置为零，从而减少神经网络中的过拟合现象。

Dropout 正则化可以提高模型的泛化能力，并防止神经元之间过度依赖。

Dropout 正则化的原理是，在训练期间以概率  随机地将一部分神经元的输出设置为零，称为“丢弃”。丢弃的方式是对每个神经元引入一个二进制的随机变量 ，取值为 0 或 1，表示该神经元是否被丢弃。在前向传播和反向传播过程中，丢弃的神经元及其连接会被忽略。

在训练过程中，Dropout 正则化的损失函数可以表示为：

在测试阶段，不再进行丢弃操作，而是将所有神经元的输出乘以概率 P。通过这种方式，Dropout 正则化可以减少神经元之间的依赖性，提高模型的鲁棒性。

下面使用Python的tensorflow库来构建一个具有Dropout正则化的简单神经网络：

import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf

# 生成一些样本数据
np.random.seed(42)
n_samples = 100
X = np.linspace(-3, 3, n_samples)
y = 0.5 * X + np.random.normal(scale=0.5, size=n_samples)

# 构建神经网络模型
model = tf.keras.models.Sequential([
    tf.keras.layers.Dense(16, activation='relu', input_shape=(1,)),
    tf.keras.layers.Dropout(0.5),
    tf.keras.layers.Dense(1)
])

# 编译和拟合模型
model.compile(optimizer='adam', loss='mean_squared_error')
model.fit(X, y, epochs=50, batch_size=16, verbose=0)

# 绘制原始数据和拟合曲线
plt.scatter(X, y, color='b', label='Original data')
plt.plot(X, model.predict(X), color='r', linewidth=2, label='Dropout Regularization')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title('Neural Network with Dropout Regularization')
plt.show()

上述代码生成了一些具有噪声的样本数据，并构建了一个简单的具有Dropout正则化的神经网络模型。通过绘制原始数据和拟合曲线，可以更好地理解Dropout正则化在神经网络中的应用。

5、贝叶斯Ridge和Lasso回归

贝叶斯Ridge回归和Lasso回归是两种基于贝叶斯统计思想的回归算法模型。它们都是经典的线性回归的扩展，可以用于特征选择和解决过拟合问题。

贝叶斯Ridge回归

贝叶斯Ridge回归通过引入正则化项来控制模型的复杂度，同时利用贝叶斯推断方法进行参数估计。其优化目标是最小化损失函数和正则化项的和。

贝叶斯Ridge回归的目标函数如下所示：

贝叶斯Ridge回归的核心思想是将权重参数视为一个随机变量，并使用贝叶斯推断对其进行估计。

通过引入先验分布p(W)，根据贝叶斯定理可以得到后验分布P(W|X,y)。然后，可以通过采样或其他方法来估计权重参数的分布，从而得到预测结果。

贝叶斯Ridge回归的优点是可以灵活地处理不同类型的数据和噪声，并且可以用作特征选择方法。缺点是计算复杂度较高，需要进行概率推断。

贝叶斯Lasso回归

贝叶斯Lasso回归也是一种基于贝叶斯统计思想的回归模型。它与贝叶斯Ridge回归类似，但使用的是L1范数正则化项。

贝叶斯Lasso回归的目标函数如下所示：

贝叶斯Lasso回归通过最小化损失函数和L1范数正则化项来实现稀疏性。L1范数倾向于将一些权重参数设为0，从而实现特征选择。

贝叶斯Lasso回归的优点是可以自动进行特征选择，并且能够处理高维数据。缺点是计算复杂度较高，需要进行概率推断。

以贝叶斯Ridge回归为例，使用Python代码实现：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import BayesianRidge

# 生成示例数据集
np.random.seed(42)
X = np.random.rand(100, 1) * 10
y = 2 * X[:, 0] + np.random.randn(100)

# 创建贝叶斯Ridge回归模型对象
model = BayesianRidge()

# 拟合模型
model.fit(X, y)

# 绘制原始数据和拟合曲线
fig, ax = plt.subplots()
ax.scatter(X, y, color='blue', label='Original data')

# 生成用于预测的新样本点
x_new = np.linspace(0, 10, 100).reshape(-1, 1)

# 预测新样本点的输出值
y_pred, y_std = model.predict(x_new, return_std=True)

# 绘制拟合曲线及置信区间
ax.plot(x_new, y_pred, color='red', label='Fitted curve')
ax.fill_between(x_new.flatten(), y_pred - y_std, y_pred + y_std, color='pink',
                alpha=0.5, label='Confidence interval')

ax.set_xlabel('X')
ax.set_ylabel('y')
ax.set_title('Bayesian Ridge Regression')
ax.legend()
plt.show()

四、组合多个弱学习器达到性能跃升的硬核集成算法

1、Bagging（自举汇聚法）

2、Boosting（提升法）

3、Stacking（堆叠法）

4、Voting（投票法）

5、深度学习集成

集成算法（Ensemble Learning）是一种将多个弱学习器组合起来形成一个强大的学习模型的方法。

通过结合多个学习器的预测结果，集成算法能够提升整体的预测性能，并且在泛化能力上通常比单个学习器更好。

下面列举常见的集成算法，先有一个大致的认识：

Bagging（自举汇聚法）：通过随机从训练集中有放回地抽取样本，构建多个基分类器，并通过投票或平均来进行最终的决策。典型的算法包括随机森林（Random Forest）。

Boosting（提升法）：按顺序训练一系列的基分类器，每个分类器根据前一个分类器的错误情况对样本权重进行调整。典型的算法包括AdaBoost、Gradient Boosting和XGBoost。

Stacking（堆叠法）：将多个不同类型的学习器组合起来，其中的元学习器用于融合基学习器的预测结果。通常采用交叉验证的方式来训练。

Voting（投票法）：基于多数表决规则，将多个独立学习器的预测结果进行投票，选取得票最多的类别作为最终的预测结果。

深度学习集成：深度学习集成是通过结合多个深度学习模型的预测结果来提升整体性能和泛化能力的方法。

集成算法的优势在于，它能够通过结合多个学习器的优点，克服单个学习器的局限性，并提高整体的预测准确性和稳定性。

集成算法还能够减少过拟合的风险，并具备一定的鲁棒性，对噪声数据和异常值的影响相对较小。

然而，在使用集成算法时也需要注意过拟合问题以及计算资源的消耗。

同时，选择适当的弱学习器和合适的集成策略也是至关重要的。

1、Bagging（自举汇聚法）

Bagging 是一种集成学习算法，它的目标是通过组合多个弱分类器来构建一个更强大的分类器。

这个算法的思想有点像“众人拾柴火焰高”的意思。

首先，从训练数据集中随机选择若干个子集，每个子集大小与原始数据集相同，但是可能包含重复的样本。然后，对每个子集使用一个基分类器进行训练，可以是决策树、支持向量机等等。这些基分类器可以并行训练，因为它们之间没有任何依赖关系。

接下来，需要进行预测时，每个基分类器都会对待分类样本进行预测。Bagging通过简单地把所有基分类器的预测结果进行平均或者投票来得出最终的预测结果。这种集成了多个分类器的方法可以减少过拟合的风险，并提高整体的预测准确性。

Bagging 有很多优势，比如它可以降低方差和偏差，并且对于噪声数据的鲁棒性较好。通过使用不同的基分类器和不同的随机子集，Bagging可以在保持模型的复杂度的同时提高预测的准确性。

下面咱们举一个例子：

假设咱们有一个关于花朵的数据集，其中包含花瓣长度、花瓣宽度等特征，以及对应的花的类别（例如玫瑰、郁金香、向日葵等）。希望使用随机森林算法进行分类，并绘制出决策边界的图形。

首先，咱们需要导入必要的库和模块。在下面使用Python实现过程中，使用scikit-learn库来实现随机森林算法，并使用matplotlib库来绘制图形，安装相应的包之后，大家可以直接运行起来。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import make_classification

# 生成一个随机的花朵数据集
X, y = make_classification(n_samples=100, n_features=2, n_informative=2, n_redundant=0,
                           n_clusters_per_class=1, random_state=42)

# 创建随机森林分类器
rf = RandomForestClassifier(n_estimators=10, random_state=42)

# 拟合数据集
rf.fit(X, y)

# 绘制决策边界
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
                     np.arange(y_min, y_max, 0.02))
Z = rf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.contourf(xx, yy, Z, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k')
plt.xlabel('Petal Length')
plt.ylabel('Petal Width')
plt.title('Random Forest Decision Boundary')
plt.show()

代码中，生成了一个随机的花朵数据集，并使用RandomForestClassifier创建了一个拥有10颗决策树的随机森林分类器。然后，绘制出决策边界的图形，其中不同的颜色代表不同的类别。

2、Boosting（提升法）

Boosting（提升法）通过反复训练一系列弱学习器（通常是决策树），然后将它们组合成一个强学习器。Boosting的基本思想是对训练样本进行加权，每次训练都已关注于之前训练中分类错误的样本，从而逐步减少整体模型的误差。

XGBoost 是 Boosting 算法的一种实现，它结合了Gradient Boosting框架和正则化技术，具有高效、灵活且易于使用的特点，并在许多Kaggle比赛等机器学习任务中取得了很好的表现。

下面是一个使用 XGBoost 进行分类任务的案例，大家可以看看~

import xgboost as xgb
import numpy as np
import matplotlib.pyplot as plt

# 创建示例数据集
X = np.random.rand(100, 2)  # 特征矩阵
y = np.random.randint(0, 2, size=100)  # 目标变量（二分类）

# 定义XGBoost参数
params = {
    'max_depth': 3,  # 决策树最大深度
    'eta': 0.1,  # 学习率
    'objective': 'binary:logistic'  # 损失函数
}

# 将数据集转换为DMatrix格式
dtrain = xgb.DMatrix(X, label=y)

# 训练XGBoost模型
model = xgb.train(params, dtrain, num_boost_round=10)

# 绘制决策边界
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
                     np.arange(y_min, y_max, 0.02))
Z = model.predict(xgb.DMatrix(np.c_[xx.ravel(), yy.ravel()]))
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('XGBoost Classifier')
plt.show()

代码中，首先创建了一个示例数据集（两个特征的二分类问题），然后定义了XGBoost的参数。

接下来，使用xgb.DMatrix将数据集转换为XGBoost所需的DMatrix格式，并训练XGBoost模型。最后，通过绘制决策边界的等高线图和散点图，展示了模型在特征空间中的分类效果。

3、Stacking（堆叠法）

Stacking（堆叠法）将多个基学习器结合在一起，使它们的预测结果作为输入来训练一个元学习器。

Stacking的基本思想是通过将不同的模型组合在一起，利用它们各自的优点来提高整体模型的性能。

下面是一个使用Stacking进行分类任务，并结合交叉验证的案例：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.model_selection import cross_val_predict
from sklearn.ensemble import StackingClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC

# 创建示例数据集
X, y = make_moons(n_samples=100, noise=0.3, random_state=42)

# 定义基学习器
estimators = [
    ('dt', DecisionTreeClassifier()),
    ('knn', KNeighborsClassifier()),
    ('svm', SVC(probability=True))
]

# 定义元学习器
meta_learner = DecisionTreeClassifier()

# 定义Stacking分类器
model = StackingClassifier(estimators=estimators, final_estimator=meta_learner)

# 交叉验证预测
y_pred = cross_val_predict(model, X, y, cv=5, method='predict_proba')

# 绘制分类效果图
plt.scatter(X[:, 0], X[:, 1], c=y_pred[:, 1], cmap='coolwarm')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('Stacking Classifier')
plt.show()

代码中，首先使用make_moons函数创建了一个示例数据集，并定义了三个基学习器（决策树、K近邻和支持向量机）和一个元学习器（决策树）。

然后，通过StackingClassifier将它们组合在一起，并设置元学习器为决策树。

接下来，使用cross_val_predict进行交叉验证预测，得到每个样本属于正类的概率。最后，通过绘制散点图，展示了模型在特征空间中的分类效果。

4、Voting（投票法）

Voting（投票法）通过将多个基学习器的预测结果进行投票或取平均来得出最终的预测结果。

Voting通常用于解决分类问题。

下面是一个使用Voting进行分类任务的案例：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import VotingClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC

# 创建示例数据集
X, y = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, random_state=42)

# 定义基学习器
estimators = [
    ('dt', DecisionTreeClassifier()),
    ('knn', KNeighborsClassifier()),
    ('svm', SVC(probability=True))
]

# 定义Voting分类器
model = VotingClassifier(estimators=estimators, voting='soft')

# 交叉验证评估
scores = cross_val_score(model, X, y, cv=5)

# 绘制性能图
plt.bar(range(1, len(scores)+1), scores)
plt.xlabel('Fold')
plt.ylabel('Accuracy')
plt.title('Voting Classifier Performance')
plt.show()

首先使用make_classification函数创建了一个示例数据集，其中包含2个特征。

然后，定义了三个基学习器（决策树、K最近邻和支持向量机）并构建了一个Voting分类器。

使用cross_val_score进行交叉验证评估，并通过绘制柱状图展示每个折叠的准确率。

实际操作中，可能需要对数据进行更详细的预处理和调整模型参数以获得更好的结果。

此外，也可以尝试使用其他类型的基学习器来构建Voting模型，以获得更好的分类性能。

5、深度学习集成

深度学习集成是指将多个深度学习模型组合起来以达到更好的预测性能或泛化能力的算法。

下面直接给出一个简单的图像分类案例、代码和使用场景来说明深度学习集成。

假设有一个图像分类任务，需要将输入的图像分为不同的类别。可以通过训练多个深度学习模型，并将它们的预测结果进行集成来提高分类性能。

import numpy as np

# 假设有3个深度学习模型，每个模型输出一个向量作为预测结果
model1_predictions = np.array([0.2, 0.6, 0.2])
model2_predictions = np.array([0.5, 0.3, 0.2])
model3_predictions = np.array([0.1, 0.1, 0.8])

# 简单平均集成：对所有模型的预测结果进行平均
ensemble_predictions = (model1_predictions + model2_predictions + model3_predictions) / 3

# 输出集成后的预测结果
print(ensemble_predictions)

深度学习集成通常使用场景可以总结为：

不同初始化条件：在深度学习中，模型的初始参数会影响其收敛性能和泛化能力。通过训练多个具有不同初始参数的模型，并将它们进行集成，可以减少模型在某些特定初始化条件下的偏差。

不同架构：通过使用不同的深度学习架构，可以捕捉到不同层次的特征。将多个具有不同架构的模型进行集成，可以提高分类或回归任务的性能。

数据增强：数据增强是一种常用的方法，通过对训练数据进行随机变换来扩充数据集。通过训练多个模型，并对它们的预测结果进行集成，可以减少数据增强引入的噪声，提高模型的鲁棒性。

需要注意的是，深度学习集成有时需要更多的计算资源和时间，因为需要训练多个模型并进行集成。另外，集成算法的选择和调优也需要经验和实践。

五、逻辑回归面试题，机器学习干货、重点。

逻辑回归是一种用于解决分类问题的统计学习方法，尤其在二分类问题中非常常见。尽管它的名称中包含”回归”一词，但实际上逻辑回归用于估计某个事物属于某一类别的概率。

逻辑回归有一些关键的点需要深入理解：

二分类问题：逻辑回归通常用于解决二分类问题，其中目标是将输入数据分为两个类别，通常表示为0和1。

逻辑函数：逻辑回归使用逻辑函数（也称为S形函数）将线性组合的特征转换为概率。这个函数将实数映射到区间[0, 1]，使其表示属于某一类别的概率。

参数估计：逻辑回归通过最大似然估计来确定模型的参数，以最大化数据的似然函数。通常使用梯度下降等优化算法来找到最佳参数。

决策边界：逻辑回归的决策边界是一个超平面，将不同类别的数据分开。在二维空间中，决策边界通常是一条曲线。

多类别问题：逻辑回归也可以扩展到多类别问题，如一对一（One-vs-One）和一对其余（One-vs-Rest）策略。

逻辑回归是一种简单而有效的分类方法，适用于许多应用，如垃圾邮件检测、疾病诊断、金融风险评估等。它具有直观的解释性，容易理解和实现

机器学习面试题，一共16大块的内容，124个问题的总结！

本文更新第二期，关于逻辑回归部分的面试题。

逻辑回归面试题 List

1、逻辑回归与线性回归有什么区别？

2、什么是逻辑回归的目标函数（损失函数）？常见的目标函数有哪些？

3、逻辑回归如何处理二分类问题？如何处理多分类问题？

4、什么是Sigmoid函数（逻辑函数）？它在逻辑回归中的作用是什么？

5、逻辑回归模型的参数是什么？如何训练这些参数？

6、什么是正则化在逻辑回归中的作用？L1和L2正则化有什么区别？

7、什么是特征工程，为什么它在逻辑回归中很重要？

8、逻辑回归的预测结果如何？怎样模型的系数（coefficient）？

9、什么是ROC曲线和AUC值？它们用来评估逻辑回归模型的哪些性能？

10、逻辑回归模型可能面临的问题有哪些？如何处理类不平衡问题？

11、什么是交叉验证，为什么在逻辑回归中使用它？

12、逻辑回归在实际应用中的一个例子是什么？描述一个应用场景，并如何使用逻辑回归来解决问题。

下面详细的将各个问题进行详细的阐述~~~~

01

1、逻辑回归与线性回归有什么区别？

逻辑回归（Logistic Regression）与线性回归（Linear Regression）是两种不同的回归方法，主要用于不同类型的问题，具有不同的模型和目标。

它们之间的主要区别，这里通过概念和公式进行对比：

1、应用领域：

线性回归通常用于解决回归问题，其中目标是预测一个连续数值输出（如房价、销售量等）。线性回归试图建立一个线性关系，以最小化观测值与模型预测值之间的差异。

逻辑回归通常用于解决分类问题，其中目标是将输入数据分为两个或多个类别（如二分类问题中的是/否、多分类问题中的类别1、类别2等）。逻辑回归使用S形函数（逻辑函数）将线性组合的输入映射到概率输出。

2、输出：

线性回归的输出是一个连续的数值，可以是任意实数。线性回归模型的公式是：

逻辑回归的输出是一个介于 0 和 1 之间的概率值，表示观测数据属于某个类别的概率。逻辑回归使用逻辑函数（也称为 sigmoid 函数）来计算概率，其公式是：

3、模型形式：

线性回归建立了一个线性关系，其中模型参数  表示输入特征与输出之间的线性关系。目标是最小化预测值与实际值之间的平方误差。

逻辑回归使用逻辑函数对线性组合进行转换，使其落在0到1之间，代表了属于某一类的概率。模型参数  表示对数概率与输入特征之间的线性关系。目标是最大化似然函数，以使观测数据在给定参数下的概率最大化。

4、目标：

线性回归的目标是找到一条最佳拟合线，以最小化实际观测值与预测值之间的误差平方和。

逻辑回归的目标是找到最佳参数，以最大化观测数据属于正类别或负类别的概率，从而能够进行分类。

线性回归和逻辑回归是两种不同类型的回归模型，用于不同类型的问题。线性回归用于预测连续数值输出，而逻辑回归用于进行二分类或多分类任务，其中输出是概率值。逻辑回归的输出受到逻辑函数的约束，使其适合处理分类问题。

021

2、什么是逻辑回归的目标函数（损失函数）？常见的目标函数有哪些？

逻辑回归的目标函数，通常也称为损失函数或代价函数，用于衡量模型的预测与实际观测值之间的差异。

逻辑回归通常用于二分类问题，其目标是最大化观测数据属于正类别或负类别的概率，从而能够进行分类。

逻辑回归的目标函数通常使用交叉熵损失函数（Cross-Entropy Loss Function）或对数损失函数（Log Loss Function），这两者通常是等价的。

逻辑回归的交叉熵损失函数：

对于二分类问题，逻辑回归的损失函数可以表示为以下形式：

其中：

 是损失函数。

 是训练样本数量。

 是第  个样本的实际类别标签（0或1）。

 是模型预测第  个样本为正类别的概率。

 是模型的参数（权重和偏置项）。

这个损失函数的目标是最小化观测数据的负对数似然（negative log-likelihood），从而最大化观测数据属于正类别或负类别的概率。

对于多分类问题，逻辑回归的损失函数可以使用多分类的交叉熵损失函数，如softmax交叉熵损失函数。

其他常见的损失函数包括均方误差损失 和平均绝对误差损失，但这些损失函数通常用于回归问题，而不是分类问题。

在分类问题中，逻辑回归的交叉熵损失函数是最常见和推荐的选择，因为它能够测量分类模型的概率输出与实际标签之间的差异，并且具有良好的数学性质。

03

3、逻辑回归如何处理二分类问题？如何处理多分类问题？

逻辑回归（Logistic Regression）是一种广泛用于处理分类问题的统计学习方法。它可以用于二分类问题和多分类问题。

处理二分类问题

对于二分类问题，逻辑回归的目标是将输入数据分为两个类别，通常表示为”0″和”1″（或”负类”和”正类”）。逻辑回归通过使用逻辑函数（也称为sigmoid函数）将线性组合的输入映射到概率输出，并根据概率来进行分类。

处理二分类问题的步骤：

1、数据准备：获取带有标签的训练数据集，其中每个样本都有一个二元类别标签，通常为0或1。

2、特征工程：根据问题的性质选择和提取适当的特征，以作为模型的输入。

3、模型训练：使用逻辑回归模型，建立一个线性组合的模型，然后通过逻辑函数将其映射到[0, 1]范围内的概率。训练模型时，通过最大化似然函数来拟合模型参数。

4、预测和分类：对于新的未标记样本，使用训练好的模型进行预测。通常，模型会输出一个概率值，然后可以根据阈值（通常为0.5）将概率转化为二元类别，例如，如果概率大于阈值，则将样本分为正类别（1），否则分为负类别（0）。

5、评估模型性能：使用适当的性能指标（如准确率、精确度、召回率、F1分数、ROC曲线和AUC）来评估模型的性能。

处理多分类问题

逻辑回归也可以用于多分类问题，其中目标是将输入数据分为三个或更多类别。

有两种主要的方法来处理多分类问题：一对多（One-vs-Rest，OvR）和Softmax回归。

1、一对多（OvR）方法：也称为一对剩余方法。对于有K个类别的问题，使用K个二分类逻辑回归模型。每个模型将一个类别作为正类别，而将其他K-1个类别视为负类别。当需要对新样本进行分类时，每个模型都会产生一个概率，最后选择具有最高概率的类别作为预测结果。

2、Softmax回归：也称为多类别逻辑回归或多项式回归。Softmax回归将多个类别之间的关系建模为一个多类别概率分布。它使用Softmax函数来将线性组合的输入映射到K个类别的概率分布，其中K是类别的数量。训练Softmax回归模型时，通常使用交叉熵损失函数。

处理多分类问题时，通常选择Softmax回归方法，因为它可以直接建模多类别之间的关系，并且在一次训练中学习所有类别的参数。一对多方法可能需要更多的模型和更多的训练时间，但在某些情况下也可以有效地处理多分类问题。

无论是处理二分类问题还是多分类问题，逻辑回归都是一个强大且常用的分类算法，可以根据问题的性质和数据集的大小来选择适当的方法。

04

4、什么是Sigmoid函数（逻辑函数）？它在逻辑回归中的作用是什么？

Sigmoid函数，也称为逻辑函数（Logistic Function），是一种常用的S型函数，具有如下的数学形式：

其中， 表示Sigmoid函数， 是自然对数的底数（约等于2.71828）， 是实数输入。

Sigmoid函数的作用在于将任何实数输入映射到一个介于0和1之间的概率值。这个映射特性使Sigmoid函数在逻辑回归中非常有用，因为它可以用来建立一个线性模型的输出，该输出表示属于某一类别的概率。

在逻辑回归中，Sigmoid函数的作用如下：

1、将线性组合转化为概率：逻辑回归模型通过将输入特征的线性组合（）传递给Sigmoid函数，将其转化为一个介于0和1之间的概率值。这个概率表示样本属于正类别的概率。

2、分类决策：通常，逻辑回归模型会根据Sigmoid函数的输出来做出分类决策。如果概率大于或等于一个阈值（通常是0.5），则样本被分类为正类别；如果概率小于阈值，则样本被分类为负类别。

3、平滑性：Sigmoid函数是光滑的S型曲线，具有连续导数。这使得逻辑回归模型易于优化，可以使用梯度下降等优化算法来找到最佳参数。

4、输出的概率解释：Sigmoid函数的输出可以被解释为一个事件的概率。这使得逻辑回归模型可以提供与概率相关的信息，而不仅仅是类别的预测结果。

Sigmoid函数在逻辑回归中的作用是将线性组合的输入映射到一个概率值，用于表示样本属于正类别的概率，并用于分类决策。这种概率性质使得逻辑回归成为二分类问题的常用算法，并且在很多其他领域中也有广泛应用。

05

5、逻辑回归模型的参数是什么？如何训练这些参数？

逻辑回归模型的参数包括权重（或系数）和截距（或偏置项），这些参数用于建立线性组合并通过Sigmoid函数将其转换为概率值。

具体来说，逻辑回归模型的参数如下：

1、权重（系数）：对应于每个输入特征的权重，用于衡量该特征对预测的影响。每个特征都有一个对应的权重参数。

2、截距（偏置项）：表示模型的基准输出，即当所有特征的值都为零时，模型的输出值。

训练逻辑回归模型的过程通常涉及以下步骤：

1、数据准备：获取带有标签的训练数据集，其中包括输入特征和相应的类别标签（通常为0或1）。

2、特征工程：选择和提取适当的特征，并进行必要的特征预处理（例如，标准化、缺失值处理等）。

3、模型初始化：初始化模型的权重和截距（通常为零或小随机值）。

4、定义损失函数：通常使用交叉熵损失函数（对数损失函数）来衡量模型预测的概率与实际标签之间的差异。

5、优化算法：选择一个优化算法，通常是梯度下降（Gradient Descent）或其变种，用于最小化损失函数并更新模型的参数（权重和截距）。优化算法会沿着损失函数的梯度方向更新参数，使损失逐渐减小。

6、训练模型：迭代运行优化算法，通过将训练数据传递给模型，计算梯度并更新参数。训练过程通常需要多个迭代轮次，直到收敛到最佳参数。

7、评估模型：使用独立的验证集或测试集来评估模型的性能。通常使用性能指标（如准确率、精确度、召回率、F1分数等）来评估模型的分类性能。

8、调整超参数：根据模型性能进行超参数调优，例如学习率、正则化参数等。

9、模型应用：一旦训练完毕并满意性能，可以使用该模型来进行新样本的分类预测。

10、可解释性分析（可选）：根据模型的参数权重，可以进行特征重要性分析，以了解哪些特征对模型的预测最具影响力。

重要的是要理解，逻辑回归的训练过程旨在找到使损失函数最小化的最佳参数组合，以使模型能够正确地估计输入特征与类别标签之间的关系，并进行二分类或多分类预测。这个过程通常使用梯度下降等优化技术来实现。

06

6、什么是正则化在逻辑回归中的作用？L1和L2正则化有什么区别？

逻辑回归中，正则化是一种用于控制模型复杂度的技术，它对模型的参数进行约束，以防止过拟合。正则化通过在损失函数中引入额外的正则化项来实现，这些正则化项对参数的大小进行惩罚。

逻辑回归中常用的正则化方法包括L1正则化和L2正则化，它们的作用是：

1、L1正则化（Lasso正则化）：

作用：L1正则化通过向损失函数添加参数的绝对值之和来惩罚模型中的大参数，从而促使一些参数变为零。这实现了特征选择，可以使模型更加稀疏，剔除不重要的特征，提高模型的泛化能力。

L1正则化项：L1正则化项的形式是 ，其中  是正则化参数， 是模型的参数。这个项在优化过程中导致一些参数  变为零，从而进行特征选择。

适用情况：L1正则化适用于高维数据集，或者当你怀疑只有少数几个特征对问题有重要影响时。

2、L2正则化（Ridge正则化）：

作用：L2正则化通过向损失函数添加参数的平方和来惩罚模型中的大参数，但不会使参数变为零，它只是压缩参数的值。L2正则化有助于减轻多重共线性问题，稳定模型的估计。

L2正则化项：L2正则化项的形式是 ，其中  是正则化参数， 是模型的参数。

适用情况：L2正则化适用于多重共线性问题，或者当你认为所有特征都对问题有一定影响时，但不希望有过大的参数。

总的来说，L1和L2正则化都有助于控制模型的复杂度，防止过拟合。它们的主要区别在于：

L1 正则化倾向于产生稀疏模型，即一些参数变为零，实现了特征选择。

L2 正则化不会使参数变为零，而是对参数进行缩小，有助于减轻多重共线性问题。

选择哪种正则化方法通常取决于数据的性质和问题的需求。在某些情况下，可以同时使用L1和L2正则化，称为弹性网络正则化，以综合两者的优点。正则化参数  的选择通常需要通过交叉验证等技术来确定。

07

7、什么是特征工程，为什么它在逻辑回归中很重要？

特征工程是机器学习和数据科学中的关键任务，它涉及选择、转换和创建特征，以便提高模型的性能和效果。

主要目标：将原始数据转化为机器学习模型可以理解和有效利用的特征表示形式。

在逻辑回归以及其他机器学习模型中，特征工程非常重要，因为它直接影响模型的性能和泛化能力。

特征工程包括以下几个方面：

1、特征选择：选择最相关和有用的特征，消除不相关的特征，以减少数据维度并提高模型的解释性。这有助于降低模型的复杂度，减少过拟合的风险。

2、特征变换：对特征进行变换，使其更适合模型的假设。例如，对数变换、标准化、归一化等变换可以使数据更符合线性模型的假设。

3、特征创建：通过组合、交叉或聚合现有特征来创建新的特征。这可以帮助模型捕获更复杂的关系和模式。

4、处理缺失值：选择合适的方法来处理缺失值，如填充缺失值、删除包含缺失值的样本等。

5、处理类别特征：将类别特征（离散型特征）进行编码，如独热编码、标签编码等，以便模型可以处理它们。

在逻辑回归中，特征工程非常重要的原因包括：

影响模型性能：逻辑回归的性能很大程度上取决于输入特征的质量和相关性。好的特征工程可以提高模型的准确性和泛化能力。

减少过拟合：精心设计的特征工程可以减少模型对训练数据的过拟合风险，从而提高模型对新数据的泛化能力。

解释性：逻辑回归通常用于解释性建模，良好的特征工程可以增加模型的可解释性，帮助理解模型的决策依据。

计算效率：精简的特征集合可以提高模型的计算效率，减少训练和推理时间。

总之，特征工程是一个关键的环节，可以极大地影响逻辑回归模型的性能和实用性。

在建立逻辑回归模型之前，务必仔细考虑和执行特征工程步骤，以确保模型能够从数据中学到有用的模式和关系。

08

8、逻辑回归的预测结果如何？怎样解释模型的系数（coefficient）？

逻辑回归的预测结果是一个介于0和1之间的概率值，表示给定输入样本属于正类别的概率。具体来说，逻辑回归模型对于输入样本的预测结果可以通过以下步骤获得：

1、线性组合：首先，模型将输入样本的特征与对应的权重（系数）相乘，然后将它们相加，得到一个实数值。这个实数值表示了线性组合的结果。

其中， 是截距（偏置项）， 是特征的权重（系数）， 是输入特征的值。

2、逻辑函数：然后，模型将线性组合的结果输入到逻辑函数（Sigmoid函数）中，将其映射到[0, 1]范围内的概率值：

预测概率线性组合

这个概率值表示输入样本属于正类别的概率。

3、分类决策：通常，可以将预测概率与一个阈值（通常为0.5）进行比较，以进行最终的分类决策。如果预测概率大于或等于阈值，则将样本分类为正类别（1），否则分类为负类别（0）。

模型的系数（权重，coefficient） 表示了每个特征对于预测结果的影响程度。系数的正负和大小告诉了我们特征对于预测是正向还是负向的影响，以及影响的相对强度。正系数表示增加该特征的值将增加样本属于正类别的概率，负系数表示增加该特征的值将减少样本属于正类别的概率。

模型的系数通常在训练过程中通过最大似然估计 或 其他优化算法来学习。系数的值可以提供有关特征的重要性和影响的信息，可以用于特征选择、可解释性分析和模型解释。系数的绝对值越大，表示对应特征的影响越显著。

09

9、什么是ROC曲线和AUC值？它们用来评估逻辑回归模型的哪些性能？

ROC曲线（Receiver Operating Characteristic Curve）和AUC值（Area Under the ROC Curve）是用于评估二分类模型性能的常用工具。

1、ROC曲线：

ROC曲线是一种图形化工具，用于可视化二分类模型的性能。它以不同的分类阈值为横轴，以真正例率（True Positive Rate，也称为召回率）为纵轴，绘制出模型在不同阈值下的性能表现。

ROC曲线的横轴表示模型的假正例率（False Positive Rate），计算方式为：假正例率 = 1 – 特异度（True Negative Rate）。

ROC曲线图中的每个点对应于不同的分类阈值，根据阈值的变化，计算真正例率和假正例率，然后绘制出曲线。ROC曲线越靠近左上角，模型性能越好。

ROC曲线的优点是不受类别不平衡问题的影响，能够展示模型在各种不同阈值下的性能表现。

2、AUC值：

AUC是ROC曲线下方的面积，被称为”Area Under the ROC Curve”。AUC值的范围通常在0.5和1之间，其中0.5表示模型的性能等同于随机猜测，1表示完美分类器。

AUC值提供了一种单一的数值度量，用于总结ROC曲线的整体性能。通常情况下，AUC值越接近1，模型的性能越好。

AUC值有一个重要的性质：如果随机选择一个正类别样本和一个负类别样本，分类器的预测概率对正负样本的排序是正确的概率（即正类别样本的预测概率大于负类别样本的预测概率）。

ROC曲线和AUC值是用于评估二分类模型性能的重要工具。它们不仅可以帮助你理解模型的表现，还可以用于比较不同模型的性能。当需要在不同分类阈值下权衡召回率和假正例率时，ROC曲线很有用。而AUC值则提供了一种简洁的方式来总结模型的性能，对于大多数分类问题都是一个有用的评估指标。

ROC曲线和AUC值用来评估逻辑回归模型在二分类问题中的以下性能方面：

1、分类准确度：虽然ROC曲线和AUC值本身并不提供分类准确度的度量，但它们可以帮助你了解模型在不同阈值下的性能表现，从而帮助你调整阈值以满足特定的分类准确度要求。通过查看ROC曲线，你可以选择一个阈值，使模型在召回率和假正例率之间达到平衡，从而满足你的分类准确度需求。

2、召回率和假正例率：ROC曲线以不同的分类阈值为横轴，分别显示了模型的召回率（True Positive Rate，也称为敏感性）和假正例率（False Positive Rate）。这对于评估模型的敏感性和特异性非常有用。高召回率表示模型能够识别出较多的正类别样本，而低假正例率表示模型能够有效控制误报。

3、模型性能比较：ROC曲线和AUC值可用于比较不同模型的性能。如果一个模型的ROC曲线位于另一个模型的上方，并且具有更高的AUC值，那么通常可以认为它在分类任务中具有更好的性能。

4、模型稳定性：通过观察ROC曲线，你可以评估模型在不同阈值下的性能稳定性。如果曲线变化不大，说明模型在不同分类阈值下都表现良好，具有稳定性。

总之，ROC曲线和AUC值是用来综合评估逻辑回归模型的分类性能、敏感性、特异性和模型稳定性的工具。它们可以帮助你理解模型在不同情境下的性能，并支持模型选择和调整分类阈值以满足特定需求。

10

10、逻辑回归模型可能面临的问题有哪些？如何处理类不平衡问题？

逻辑回归模型可能面临的一些问题包括：

1、类不平衡问题：当正类别和负类别的样本数量差异很大时，模型可能倾向于偏向于多数类，而忽略少数类。这会导致模型的性能不均衡，对少数类的识别能力较弱。

2、多重共线性：当特征之间存在高度相关性时，逻辑回归模型的参数估计可能变得不稳定，导致难以解释的结果。

3、过拟合：如果模型过于复杂或特征数量过多，逻辑回归模型可能过拟合训练数据，表现良好的泛化能力较差。

4、特征选择：选择合适的特征对模型性能至关重要。错误的特征选择可能导致模型性能下降。

5、阈值选择：逻辑回归模型的输出是一个概率值，需要选择合适的阈值来进行分类决策，不同的阈值可能导致不同的性能表现。

如何处理类不平衡问题：

处理类不平衡问题是逻辑回归模型常见的挑战之一。

以下是一些处理类不平衡问题的方法：

1、重采样：

过采样：增加少数类的样本数量，可以通过复制已有的少数类样本或生成合成样本来实现。

欠采样：减少多数类的样本数量，可以通过删除一些多数类样本来实现。

合成采样：结合过采样和欠采样策略，以平衡样本分布。

2、使用不同的类权重：

通过设置类别权重参数，赋予不同类别的样本不同的权重，以便模型更已关注少数类。在许多机器学习框架中，可以使用参数来调整类别权重。

3、生成合成样本：

利用生成对抗网络（GANs）或其他合成数据生成方法，生成合成的少数类样本，以平衡类别分布。

4、集成方法：

使用集成方法如随机森林、梯度提升树等，这些方法对类不平衡问题具有较强的鲁棒性。

5、改变阈值：

调整分类阈值，以便更好地适应类别不平衡问题。通常情况下，减小阈值可以增加对少数类的识别能力。

6、使用不同的评估指标：

使用类别不平衡问题友好的评估指标，如准确率、精确度、召回率、F1分数、ROC曲线和AUC值等，以更全面地评估模型性能。

最佳的处理类不平衡问题的方法取决于具体情况和数据集的性质。通常，需要尝试不同的方法并评估它们的效果，以找到最适合特定问题的方法。

11

11、什么是交叉验证，为什么在逻辑回归中使用它？

交叉验证是一种评估机器学习模型性能的统计技术。它将数据集分成训练集和测试集的多个子集，然后多次训练和测试模型，以便更全面地评估模型在不同数据子集上的性能表现。

交叉验证的主要目的是：

1、评估模型泛化能力：交叉验证可以帮助我们评估模型在未见过的数据上的性能，而不仅仅是在训练数据上的性能。这有助于检测模型是否过拟合或欠拟合。

2、减少随机性：将数据集分成多个子集并多次训练模型，有助于减少随机性对性能评估的影响。这使得我们能够更可靠地评估模型的性能。

在逻辑回归中使用交叉验证的原因包括：

1、模型选择：交叉验证可以帮助选择逻辑回归模型的超参数，如正则化参数（如L1或L2正则化的强度）。通过在不同的数据子集上进行验证，可以找到使模型性能最优的参数配置。

2、性能评估：交叉验证提供了一个更准确的模型性能评估方法，以便在不同数据子集上评估模型的性能。这有助于识别模型是否具有一般化能力，以及是否需要进一步改进。

3、处理数据不平衡：如果数据集中存在类不平衡问题，交叉验证可以确保在每个数据子集上都有足够的正类别和负类别样本，从而更准确地评估模型的性能。

4、可解释性：逻辑回归通常用于可解释性建模，而交叉验证可以帮助确定哪些特征对模型性能具有重要影响，从而增强了模型的可解释性。

常见的交叉验证方法包括k折交叉验证（k-fold cross-validation）、留一交叉验证（leave-one-out cross-validation，LOOCV）等。k折交叉验证将数据集分成k个子集，其中k-1个子集用于训练，剩余的1个子集用于测试，这一过程重复k次，每个子集都有机会充当测试集。最后，计算k次测试的平均性能来评估模型。交叉验证通常是在机器学习中评估模型性能的重要步骤，有助于更可靠地了解模型的表现。

咱们详细说下k折交叉验证。

k折交叉验证用于评估机器学习模型的性能。它将数据集分成k个近似相等的子集（通常是5或10），然后进行k次模型训练和性能评估，每次选择一个子集作为验证集，其余子集用于训练模型。这个过程的目标是确保每个子集都充当过验证集，以便全面评估模型的性能。

以下是使用Python的Scikit-Learn库来执行k折交叉验证的示例：

from sklearn.model_selection import cross_val_score, KFold
from sklearn.linear_model import LogisticRegression

# 创建一个逻辑回归模型
model = LogisticRegression()

# 创建k折交叉验证对象，这里设置k=5
kfold = KFold(n_splits=5, shuffle=True, random_state=42)

# 使用cross_val_score执行交叉验证并评估模型性能
scores = cross_val_score(model, X, y, cv=kfold, scoring='accuracy')

# 打印每次交叉验证的准确度分数
print("Cross-Validation Scores:", scores)

# 打印平均准确度分数
print("Average Accuracy:", scores.mean())

上述代码中，首先创建了一个逻辑回归模型（LogisticRegression），然后创建了一个k折交叉验证对象（KFold），将数据分为5个子集，并在每次交叉验证中随机打乱数据（shuffle=True）。接下来，我们使用cross_val_score函数执行交叉验证，评估模型的性能，并将每次交叉验证的准确度分数存储在scores数组中。最后，计算并打印平均准确度分数。

使用k折交叉验证可以更全面地了解模型在不同数据子集上的性能表现，有助于检测模型是否过拟合或欠拟合，以及确定模型的稳定性。这是模型选择和调优的重要步骤之一。

12

12、逻辑回归在实际应用中的一个例子是什么？描述一个应用场景，并如何使用逻辑回归来解决问题。

逻辑回归在实际应用中有许多用途，其中一个典型的应用是二分类问题，如信用风险评估。

下面咱们举一个信用风险评估的应用场景，并描述如何使用逻辑回归来解决问题。

应用场景：信用风险评估

问题描述：一家银行想要评估客户申请信用卡的风险，以决定是否批准他们的信用卡申请。银行需要预测每位申请者是否会在未来的一年内违约（无法按时偿还信用卡债务）。这是一个典型的二分类问题，其中正类别表示违约，负类别表示未违约。

解决方法：

1、数据收集：首先，银行需要收集历史客户的数据，包括客户的个人信息（如年龄、性别、婚姻状况等）、财务信息（如收入、支出、债务等）、以及与信用卡使用相关的数据（如信用卡账户余额、信用额度、逾期次数等）。

2、数据预处理：对数据进行清洗和预处理，包括处理缺失值、异常值、类别特征的编码等。还需要进行特征选择，选择与信用风险相关的特征。

3、数据划分：将数据集分为训练集和测试集。通常，将大部分数据用于训练模型，剩余的一部分用于评估模型性能。

4、建立逻辑回归模型：使用训练数据建立逻辑回归模型。模型的输入特征是客户的个人和财务信息，输出是二分类的违约/未违约标签。

5、模型训练：通过训练数据对逻辑回归模型的参数进行估计，通常使用最大似然估计等方法来完成。

6、模型评估：使用测试数据来评估模型的性能。可以使用各种评估指标如准确率、召回率、F1分数、ROC曲线和AUC值来衡量模型的性能。

7、阈值选择：根据业务需求，选择合适的分类阈值，以平衡风险和收益。不同的阈值会影响模型的预测结果。

8、模型部署：一旦满足性能要求，可以将逻辑回归模型部署到生产环境中，用于自动评估信用卡申请的风险。

9、持续监控和改进：定期监控模型的性能，根据新的数据和反馈进行模型的改进和更新，以确保其持续有效。

逻辑回归在信用风险评估中的应用是一个典型的二分类问题，它可以帮助银行自动化信用卡申请的批准过程，提高风险管理效率，并减少不良债务的风险。这是逻辑回归在金融领域中的一个实际应用示例。

以下是一个简单的Python案例，演示如何使用逻辑回归模型来解决信用风险评估问题。这个案例使用了Scikit-Learn库中的示例数据集，用于预测信用卡申请者是否具有高风险。

import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix

# 读取数据集
data = pd.read_csv('credit_data.csv')  # 假设数据集以CSV格式存在

# 处理NaN值，使用特征列的均值填充NaN值
data.fillna(data.mean(), inplace=True)

# 分割特征和标签
X = data.iloc[:, :-1]  # 特征
y = data.iloc[:, -1]  # 标签

# 数据标准化
scaler = StandardScaler()
X = scaler.fit_transform(X)

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 建立逻辑回归模型
model = LogisticRegression()

# 模型训练
model.fit(X_train, y_train)

# 模型预测
y_pred = model.predict(X_test)

# 评估模型性能
accuracy = accuracy_score(y_test, y_pred)
confusion = confusion_matrix(y_test, y_pred)
classification_report_str = classification_report(y_test, y_pred)

# 打印模型性能指标
print("Accuracy:", accuracy)
print("Confusion Matrix:
", confusion)
print("Classification Report:
", classification_report_str)

代码中，首先加载示例数据集（名为credit_data.csv的数据集），然后进行数据预处理，包括特征标准化。接下来，我们将数据集分为训练集和测试集，然后建立逻辑回归模型，对模型进行训练，并用测试集进行模型评估。最后，我们打印了模型的准确度、混淆矩阵和分类报告。

这个简单的示例演示了如何使用逻辑回归模型来解决信用风险评估问题，以预测信用卡申请者的高风险。在实际应用中，可以使用真实的数据集和更多的特征来构建更复杂的信用风险评估模型。

六、聚类算法的作用和怎么用

 大部分人对聚类的认识可以归纳为以下几个方面：

数据分组：许多人将聚类视为将数据划分为不同的组或簇，使得同一组内的数据点更加相似或相关。这种观点认为聚类是一种无监督学习技术，用于发现数据中的内在结构和模式。

相似性度量：通常认为聚类算法通过计算数据点之间的相似性或距离来确定它们是否属于同一簇。相似性度量可以基于欧氏距离、余弦相似度等方法。

发现未知群体：聚类被视为一种工具，用于发现现有数据中隐藏的未知群体。通过聚类分析，可以发现数据集中的潜在模式、群体或类别，从而帮助了解数据的特征和结构。

应用领域：人们普遍认为聚类广泛应用于各个领域，如市场细分、客户分析、图像分割、推荐系统等。聚类可以帮助理解和利用大规模数据集，探索数据中的关联性和趋势。

然而，值得注意的是，不同人对聚类的认识和理解可能存在差异，因为聚类本质上是一个多样化的领域，涉及多种算法和技术。此外，聚类也可能面临一些挑战，如选择合适的距离度量、确定最佳簇的数量等。因此，在使用聚类算法时，需要根据具体问题和数据特点进行适当的选择和调整。

今天就来详细说说常见的几种：

K均值聚类

层次聚类

密度聚类

谱聚类

EM聚类

模糊聚类

以下代码均可直接运行起来，方便学习！

K均值聚类

K均值聚类是一种常用的无监督学习算法，用于将数据点划分为不同的簇，使得同一簇内的数据点彼此相似度较高，不同簇之间的数据点相似度较低。

这个算法的目标是将数据点分为K个簇，其中K是用户定义的参数。K均值聚类的原理相对简单，主要思想是通过迭代寻找K个簇的中心点，将每个数据点分配给距离其最近的中心点，然后更新中心点的位置，直到满足停止条件为止。

原理介绍

1、选择要分成的簇的数量K。

2、随机初始化K个中心点，这些中心点可以是从数据集中随机选择的数据点。

3、重复以下过程，直到满足停止条件：

将每个数据点分配到距离其最近的中心点所属的簇。

对每个簇，计算所有数据点的平均值，并将其作为新的中心点。

停止条件通常可以是以下之一：

中心点不再改变或改变非常小。

数据点不再改变其所属簇。

公式表达

K均值聚类的主要公式包括：

距离度量（一般使用欧氏距离）：

对于两个数据点X和Y，它们之间的欧氏距离可以表示为：

一个案例

一个用Python实现K均值聚类：

import numpy as np
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt

# 生成随机数据
np.random.seed(0)
X = np.random.rand(100, 2)

# 使用K均值聚类，假设要分成3个簇
kmeans = KMeans(n_clusters=3)
kmeans.fit(X)

# 获取簇的中心点和每个数据点的所属簇
centers = kmeans.cluster_centers_
labels = kmeans.labels_

# 绘制数据点和簇中心
plt.scatter(X[:, 0], X[:, 1], c=labels)
plt.scatter(centers[:, 0], centers[:, 1], marker='x', s=200, linewidths=3, color='r')
plt.title('K-Means Clustering')
plt.show()

这段代码首先生成一些随机数据，然后使用scikit-learn库的KMeans类进行聚类，并绘制了数据点和簇中心的图形。

可以看到K均值聚类是如何将数据点分成不同的簇的，并找到簇的中心点。图形展示了数据点的分布以及簇中心的位置。

层次聚类

层次聚类 通过构建数据点之间的层次结构来组织簇。这种层次结构通常以树状图（树状图或谱系图）的形式呈现，可以帮助理解数据点之间的相似性关系以及簇之间的关系。

层次聚类可以分为两种主要类型：自上而下的凝聚聚类和自下而上的分裂聚类。

原理介绍

凝聚聚类（Agglomerative Clustering）：从底部开始，每个数据点被视为一个单独的簇，然后迭代地合并最接近的簇，直到只剩下一个大的簇。

分裂聚类（Divisive Clustering）：从顶部开始，所有数据点被视为一个大的簇，然后逐渐分裂成更小的簇，直到每个数据点都是一个单独的簇。

层次聚类的主要步骤包括：

初始化：将每个数据点视为一个独立的簇。

合并（对于凝聚聚类）或分裂（对于分裂聚类）簇以创建一个新的层次结构。

重复步骤2，直到满足停止条件。

公式表达

在层次聚类中，距离度量是关键。常用的距离度量包括欧氏距离、曼哈顿距离、马氏距离等，具体选择取决于问题的性质。合并或分裂簇的准则也可以有多种，例如最短距离、最长距离、平均距离等。

一个Python案例

使用 scikit-learn 实现层次聚类：

import numpy as np
from sklearn.cluster import AgglomerativeClustering
import matplotlib.pyplot as plt
from scipy.cluster.hierarchy import dendrogram

# 生成随机数据
np.random.seed(0)
X = np.random.rand(10, 2)

# 使用凝聚聚类，假设要分成2个簇
agg_clustering = AgglomerativeClustering(n_clusters=2)
agg_clustering.fit(X)

# 绘制树状图（谱系图）
linkage_matrix = np.column_stack([agg_clustering.children_, agg_clustering.distances_])
dendrogram(linkage_matrix, p=10, truncate_mode='level')

plt.title('Hierarchical Clustering Dendrogram')
plt.xlabel('Data point index')
plt.ylabel('Distance')
plt.show()

首先生成一些随机数据，然后使用scikit-learn库的AgglomerativeClustering类进行凝聚聚类，并绘制了树状图（谱系图）。树状图显示了数据点的分层结构，以及簇之间的合并情况。

密度聚类

密度聚类 根据数据点周围的密度来发现簇。最著名的密度聚类算法之一是DBSCAN（Density-Based Spatial Clustering of Applications with Noise）。

DBSCAN是一种基于密度的聚类算法，它的主要思想是根据数据点周围的密度来确定簇的边界。

与K均值等算法不同，DBSCAN不需要事先指定簇的数量，而且能够发现各种形状的簇，同时还能识别异常点（噪声）。

原理介绍

DBSCAN 算法的核心思想是通过以下两个参数来定义簇：

1、**ε (epsilon)**：表示半径，它用来确定一个点的邻域范围。

2、MinPts：表示一个点的邻域内至少包含的数据点数目。

DBSCAN 算法的工作流程如下：

1、随机选择一个未被访问的数据点作为起始点。

2、计算该点的ε邻域内的数据点数量。

3、如果邻域内的数据点数目大于等于MinPts，则将该点标记为核心点（Core Point），并将其邻域内的所有点加入同一簇中。

4、重复以上过程，直到无法找到更多的核心点。

5、选择下一个未被访问的数据点，继续上述过程，直到所有数据点都被访问。

最终，所有被访问的点都将属于某个簇或者被标记为噪声点。

关键概念

ε邻域：对于点P，它的ε邻域包含了距离点P不超过ε的所有点。

核心点（Core Point）：如果点P的ε邻域内至少包含MinPts个数据点，那么点P被标记为核心点。

边界点（Border Point）：如果点P的ε邻域内包含少于MinPts个数据点，但它是某个核心点的邻接点，那么点P被标记为边界点。

噪声点（Noise Point）：如果点P不是核心点，也不是边界点，那么点P被标记为噪声点。

一个案例

使用 Scikit-Learn 中的DBSCAN 做一个密度聚类。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import DBSCAN
from sklearn.datasets import make_blobs

# 创建一个随机数据集
X, _ = make_blobs(n_samples=1000, centers=3, cluster_std=1.0, random_state=42)

# 使用DBSCAN算法进行密度聚类
dbscan = DBSCAN(eps=0.5, min_samples=5)
dbscan.fit(X)

# 获取每个点的簇标签
labels = dbscan.labels_

# 绘制聚类结果
unique_labels = np.unique(labels)
colors = plt.cm.Spectral(np.linspace(0, 1, len(unique_labels)))

for label, color in zip(unique_labels, colors):
    if label == -1:
        # 噪声点用黑色表示
        color = 'k'
    
    class_member_mask = (labels == label)
    xy = X[class_member_mask]
    plt.scatter(xy[:, 0], xy[:, 1], c=color, s=20, label='Cluster %d' % label)

plt.title('DBSCAN Clustering')
plt.legend()
plt.show()

这个示例使用了Scikit-Learn中的DBSCAN类来对一个具有3个簇的数据集进行聚类。

实际情况中，可以根据自己的数据和参数来调整代码以适应不同的情况。

谱聚类

谱聚类 通过将数据集表示为图的形式来进行聚类分析。

谱聚类在图论、线性代数和谱分析等领域有广泛的应用，它能够有效地处理复杂的数据结构，并且在一些情况下表现出色。

原理介绍

1、构建相似度图（Affinity Matrix）：首先，将数据集中的样本视为图的节点，计算每一对样本之间的相似度。通常使用高斯核函数来度量相似性，具体计算方式如下：

一个Python案例

依旧使用 Scikit-Learn 进行实现：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.cluster import SpectralClustering
from sklearn.metrics import pairwise_distances
from scipy.sparse import csgraph

# 生成一个随机的月亮形状的数据集
X, _ = make_moons(n_samples=1000, noise=0.05, random_state=42)

# 计算相似度矩阵
sigma = 0.2
W = np.exp(-pairwise_distances(X, metric="sqeuclidean") / (2.0 * sigma ** 2))

# 构建对称归一化拉普拉斯矩阵
D = np.diag(W.sum(axis=1))
L = D - W
D_sqrt_inv = np.linalg.inv(np.sqrt(D))
L_sym = np.dot(np.dot(D_sqrt_inv, L), D_sqrt_inv)

# 计算特征向量
k = 2  # 聚类数
eigenvalues, eigenvectors = np.linalg.eigh(L_sym)
X_new = eigenvectors[:, :k]

# 使用谱聚类
sc = SpectralClustering(n_clusters=k, affinity="precomputed", random_state=42)
labels = sc.fit_predict(W)

# 可视化结果
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap="viridis")
plt.title("Spectral Clustering Result")
plt.subplot(1, 2, 2)
plt.scatter(X[:, 0], X[:, 1], c=_, cmap="viridis")
plt.title("Original Data")
plt.show()

首先生成一个月亮形状的数据集，然后计算相似度矩阵，构建对称归一化拉普拉斯矩阵，计算特征向量，最后使用谱聚类对数据集进行聚类，并可视化聚类结果和原始数据。

七、机器学习：在Python中sklearn库的使用

以下是 6 个重要的无监督学习算法，这些算法都可以通过使用sklearn（Scikit-learn）库在Python中很好地处理：

目录

K-Means 聚类

层次聚类

DBSCAN

主成分分析

独立成分分析

高斯混合模型

K-Means 聚类

数据准备

首先，我们导入必要的库和数据，并进行基本的数据探查。

这里，准备了名称为「customer_data.csv」的数据集，维度分别为“Age, Annual_Income 和Spending_Score`作为 3 个特征。

获取数据集：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
from sklearn.preprocessing import StandardScaler
from time import time

# 假定你已将上文的数据存储为'customer_data.csv'
data = pd.read_csv("customer_data.csv")

数据标准化

因为K-Means聚类是距离基础的算法，我们通常在进行聚类分析之前会标准化我们的数据。

scaler = StandardScaler()
scaled_data = scaler.fit_transform(data)

确定K值

这里我们使用轮廓系数（Silhouette Score）来帮助我们确定适当的K值。

轮廓系数是在-1到1之间的，一个高的轮廓系数表明样本点离其他类的距离较远。

k_values = range(2, 11)
silhouette_scores = []

for k in k_values:
    kmeans = KMeans(n_clusters=k, random_state=42)
    kmeans.fit(scaled_data)
    silhouette_scores.append(silhouette_score(scaled_data, kmeans.labels_))

plt.plot(k_values, silhouette_scores, marker='o')
plt.title('Silhouette Score for Different k')
plt.xlabel('k')
plt.ylabel('Silhouette Score')
plt.show()

模型训练

从轮廓系数图中选择一个合适的 K 值进行模型训练，并可视化结果。

# 假设我们选择k=3
k = 3
kmeans = KMeans(n_clusters=k, random_state=42)
clusters = kmeans.fit_predict(scaled_data)

# 可视化结果
plt.scatter(scaled_data[clusters == 0, 0], scaled_data[clusters == 0, 1], label='Cluster 1')
plt.scatter(scaled_data[clusters == 1, 0], scaled_data[clusters == 1, 1], label='Cluster 2')
plt.scatter(scaled_data[clusters == 2, 0], scaled_data[clusters == 2, 1], label='Cluster 3')
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s=300, c='red', label='Centroids')
plt.title('Clusters of Customers')
plt.xlabel('Age (scaled)')
plt.ylabel('Spending Score (scaled)')
plt.legend()
plt.show()

这三个群集可能分别代表以下客户类型：

Cluster 1: 年轻且花费适中的客户群体

Cluster 2: 年轻且花费较高的客户群体

Cluster 3: 年纪较大且花费较低的客户群体

商业决策将基于这些群体的特点来制定。例如，针对花费较高的年轻客户群体，可以提供最新的产品推广或者特殊折扣，以便进一步激励他们的购买行为。

以上代码及分析基于假定的数据。在现实项目中，要充分理解业务背景、数据的含义并根据业务目标来决定聚类的数量及如何解读各个群体的特征。

层次聚类

为了便于展示，我们使用上文中的customer_data.csv数据。我们将使用层次聚类（Hierarchical Clustering）探索数据内在的群集结构。

咱们已关注的特征依然是Age, Annual_Income, 和Spending_Score。

数据准备

如之前例子一样，首先进行数据导入和标准化。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.cluster.hierarchy import dendrogram, linkage
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import AgglomerativeClustering

# 读取数据
data = pd.read_csv("customer_data.csv")

# 数据标准化
scaler = StandardScaler()
scaled_data = scaler.fit_transform(data)

层次聚类模型

构建并可视化树状图 (Dendrogram)

我们用scipy中的linkage和dendrogram函数来构建层次聚类的树状图。

linked = linkage(scaled_data, 'ward')  # 使用Ward连接方法

plt.figure(figsize=(10, 7))
dendrogram(linked,
           orientation='top',
           labels=data.index,
           distance_sort='descending',
           show_leaf_counts=True)
plt.show()

训练模型并可视化结果

选择一个合适的距离阈值或群集数量进行模型训练，并可视化结果。

# 定义模型并指定我们想要的群集数量
cluster = AgglomerativeClustering(n_clusters=3, affinity='euclidean', linkage='ward')  

# 训练模型并预测标签
cluster_labels = cluster.fit_predict(scaled_data)

# 可视化结果
plt.figure(figsize=(10, 7))
plt.scatter(scaled_data[:,0], scaled_data[:,1], c=cluster_labels, cmap='rainbow')
plt.title('Clusters of Customers')
plt.xlabel('Age (scaled)')
plt.ylabel('Spending Score (scaled)')
plt.show()

与K-Means聚类类似，我们可以根据生成的群集进行进一步分析。例如，每个群集的中心的特征可以被认为是该群集的“代表”特征。由于我们使用了相同的特征（Age和Spending_Score），群集的解释将与前文类似。

注意点

1、距离计算：affinity参数表示用于计算距离的方法。在本例中，我们使用了欧几里得距离。

2、链接方法：linkage参数表示用于链接群集的方法。在本例中，我们使用了Ward方法，该方法试图最小化群集内的方差。

3、选择群集数量：在生成的树状图中，通常选择一个“高度”来切割树形结构，并形成各个群集。在这个示例中，我们预先选择了群集的数量。在实际分析中，你也可以选择在树状图中一个合适的高度来切割群集。

DBSCAN

咱们继续使用customer_data.csv数据集来演示DBSCAN。

数据准备

DBSCAN模型构建与训练

首先选定DBSCAN的两个主要参数：邻域大小（eps）和最小点数（min_samples）。

# 实例化DBSCAN模型
dbscan = DBSCAN(eps=0.5, min_samples=5)

# 训练模型
clusters = dbscan.fit_predict(scaled_data)

# 计算轮廓系数
print(f'Silhouette Score: {silhouette_score(scaled_data, clusters):.2f}')

结果可视化

我们用散点图展示聚类的结果。

# 可视化
plt.scatter(scaled_data[:,0], scaled_data[:,1], c=clusters, cmap='plasma')
plt.title('DBSCAN Clustering')
plt.xlabel('Age (scaled)')
plt.ylabel('Spending Score (scaled)')
plt.show()

轮廓系数：展示了群集的密度和分离度。范围从-1到1，值越高表明聚类效果越好。由于DBSCAN能够识别噪声，轮廓系数可能会受到噪声点的影响。

图形分析：可视化结果允许我们直观地看到不同的群集及其形状。DBSCAN能够找到非球形的群集，这是其独有的优点。

注意点

参数选择：eps和min_samples的选择对模型影响很大。一个常见的方法是使用k-距离图来估计eps。通常需要多次尝试来找到合适的参数。

标准化的重要性：由于DBSCAN依赖于距离的计算，所以标准化通常是必需的。

处理不均衡数据：DBSCAN可能在不同密度的群集之间表现不佳。在数据的分布非常不均匀时，可能需要调整参数或选择其他算法。

噪声点：DBSCAN将不属于任何群集的点归类为噪声（即，将其标签为-1）。在结果解释和进一步分析时需要注意这一点。

DBSCAN提供了一种不需要预先指定群集数量的聚类方法，并且可以找到复杂形状的群集。然而，它对参数的选择非常敏感，需要仔细进行调整和验证。

主成分分析

主成分分析（PCA）是一种在降维和可视化高维数据方面非常流行的技术。通过找到数据的主轴并将数据投影到这些轴上来减少数据的维度，从而尽可能保留数据的方差。

数据准备

假设我们有一个包含3个特征的 150×3 的数据集。我们的目标是将这些数据从3D空间降维到2D空间以便进行可视化。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler

# 使用iris数据集
iris = load_iris()
X = iris.data  # 特征矩阵, shape: (150, 4)
y = iris.target  # 目标变量, shape: (150,)

# 标准化数据
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

模型训练

# 实施PCA
pca = PCA(n_components=2)  # 我们将数据投影到前两个主成分
X_pca = pca.fit_transform(X_scaled)

数据可视化

# 创建一个新的figure
plt.figure(figsize=(8,6))

# 遍历标签，为不同的标签创建不同的散点图
for target, color in zip(iris.target_names, ['r', 'g', 'b']):
    indicesToKeep = iris.target == np.where(iris.target_names == target)[0][0]
    plt.scatter(X_pca[indicesToKeep, 0], 
                X_pca[indicesToKeep, 1], 
                c = color, 
                s = 50)

# 增加图例和坐标轴的标签
plt.legend(iris.target_names, loc='upper right', fontsize='x-large')
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.title('2D PCA of Iris Dataset')
plt.grid(True)

# 显示图形
plt.show()

解释方差

explained_variance = pca.explained_variance_ratio_
print(f"Explained variance: {explained_variance}")

从上面的2D散点图中，你可以看到3种不同的鸢尾花在投影到前两个主成分上时是如何分开的。另外，解释的方差告诉我们前两个主成分保存了多少原始数据的方差。在许多情况下，希望这些主成分包含了足够多的信息，以便在丢失最小量的信息的情况下利用它们。

这个简单的示例展示了PCA的工作方式和它如何在实践中实施。

独立成分分析

独立成分分析是一种用于从混合信号中恢复原始信号的技术，通常用于盲源分离和信号处理。

数据准备

首先，我们需要准备一个包含混合信号的虚拟数据集。

以下示例中，创建两个独立的信号并将它们线性混合。

import numpy as np

# 创建两个独立的信号
signal_1 = np.random.rand(1000)
signal_2 = np.sin(np.linspace(0, 100, 1000))

# 创建混合信号
mixing_matrix = np.array([[2, 1], [1, 2]])  # 混合矩阵
mixed_signals = np.dot(np.vstack((signal_1, signal_2)).T, mixing_matrix.T)

ICA模型训练

使用Scikit-Learn中的FastICA来拟合ICA模型，以恢复原始信号。

from sklearn.decomposition import FastICA

ica = FastICA(n_components=2)
recovered_signals = ica.fit_transform(mixed_signals)

绘制混合信号和恢复信号的图形

我绘制混合信号和恢复信号的图形，以可视化ICA的效果。

import matplotlib.pyplot as plt

# 绘制混合信号
plt.figure(figsize=(12, 6))
plt.subplot(2, 2, 1)
plt.plot(signal_1, label='Signal 1')
plt.title('Original Signal 1')
plt.subplot(2, 2, 2)
plt.plot(signal_2, label='Signal 2')
plt.title('Original Signal 2')

# 绘制混合信号
plt.subplot(2, 2, 3)
plt.plot(mixed_signals[:, 0], label='Mixed Signal 1')
plt.title('Mixed Signal 1')
plt.subplot(2, 2, 4)
plt.plot(mixed_signals[:, 1], label='Mixed Signal 2')
plt.title('Mixed Signal 2')

plt.tight_layout()

# 绘制恢复信号
plt.figure(figsize=(12, 6))
plt.subplot(2, 1, 1)
plt.plot(recovered_signals[:, 0], label='Recovered Signal 1')
plt.title('Recovered Signal 1')
plt.subplot(2, 1, 2)
plt.plot(recovered_signals[:, 1], label='Recovered Signal 2')
plt.title('Recovered Signal 2')

plt.tight_layout()
plt.show()

在图形中，可以看到原始信号、混合信号以及通过ICA恢复的信号。恢复信号应该与原始信号尽可能接近，这就是ICA的目标。通过独立成分分析，我们可以从混合信号中分离出原始信号，实现了信号的盲源分离。

示例演示了独立成分分析的用途，如何准备数据，训练模型以及通过图形可视化来理解分离效果。在实际应用中，你可以使用不同数量的混合信号和独立成分来执行ICA，以满足具体的应用需求。

高斯混合模型

高斯混合模型是一种用于建模多个高斯分布混合在一起的概率模型。

下面是一个关于高斯混合模型的完整示例，包括数据准备、模型训练、Python代码和图形展示等等。

数据准备

首先，我们需要准备一个包含多个高斯分布的虚拟数据集。

例子中，创建一个包含两个高斯分布的数据集。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.mixture import GaussianMixture

# 创建两个高斯分布的虚拟数据集
np.random.seed(0)
data1 = np.random.normal(0, 1, 200)
data2 = np.random.normal(5, 1, 200)
data = np.concatenate((data1, data2), axis=0)

# 绘制数据分布
plt.hist(data, bins=30, density=True, alpha=0.5)
plt.title('Data Distribution')
plt.xlabel('Value')
plt.ylabel('Density')
plt.show()

GMM模型训练

接下来，我们将使用Scikit-Learn中的GaussianMixture来拟合GMM模型，以对数据进行建模。

# 使用GMM拟合数据
gmm = GaussianMixture(n_components=2, random_state=0)
gmm.fit(data.reshape(-1, 1))

绘制GMM模型的图形

我们可以绘制GMM模型对数据的拟合情况，以及估计的高斯分布参数。

# 绘制数据分布
plt.hist(data, bins=30, density=True, alpha=0.5, label='Data')

# 绘制GMM模型的拟合曲线
x = np.linspace(-3, 8, 1000)
pdf = np.exp(gmm.score_samples(x.reshape(-1, 1)))
plt.plot(x, pdf, '-r', label='GMM')

# 绘制每个高斯分布的拟合曲线
for i in range(2):
    mean = gmm.means_[i][0]
    variance = np.sqrt(gmm.covariances_[i][0][0])
    weight = gmm.weights_[i]
    plt.plot(x, weight * np.exp(-(x - mean)**2 / (2 * variance**2)) / (np.sqrt(2 * np.pi) * variance),
             label=f'Component {i+1}')

plt.title('Gaussian Mixture Model Fit')
plt.xlabel('Value')
plt.ylabel('Density')
plt.legend()
plt.show()

在图中，你可以看到原始数据的分布（直方图），以及GMM模型的拟合曲线。GMM模型通过多个高斯分布的线性组合来拟合数据分布，图中还显示了每个高斯分布的拟合曲线，包括均值、方差和权重。

七、深度学习各算法的优缺点和适用场景

这个示例演示了如何使用高斯混合模型来对数据进行建模和拟合，以及如何通过图形可视化来理解模型的效果。在实际应用中，你可以根据数据的特性和需求选择不同数量的高斯分布成分来建立更复杂的模型。

深度学习通过多层神经网络模型来学习和表示数据的高级特征。

这些神经网络通常包括多个隐层，因此被称为“深度”学习。

深度学习现在的重要作用是大家有目共睹的。

先来简单来聊聊在算法领域和实际工业领域都发挥了哪些重要的作用。

在算法领域：

1、模式识别和分类：深度学习可以用于解决复杂的模式识别问题，如图像分类、语音识别和自然语言处理。深度卷积神经网络 和 循环神经网络等模型在这些任务中取得了巨大的成功。

2、生成模型：深度学习可用于生成新的数据，包括图像、文本和音频。生成对抗网络和变分自编码器等生成模型已经被广泛应用于图像生成、自然语言生成和音乐合成等任务。

3、强化学习：深度强化学习在智能决策和控制领域取得了显著进展。它被用于构建智能体（Agents）来完成各种任务，如自动驾驶、机器人控制和游戏策略。

4、推荐系统：深度学习在个性化推荐系统中扮演着关键角色，可以更好地理解用户兴趣和行为，从而提供更准确的推荐。

5、自然语言处理：深度学习已经取得了在文本分析、机器翻译、情感分析等领域的重大突破，使计算机能够更好地理解和生成自然语言。

在实际工业领域：

1、计算机视觉：深度学习在工业领域中的计算机视觉应用非常非常广泛。可以用于质检、对象检测、图像分类、自动驾驶和医学图像分析等任务。

2、自然语言处理：深度学习模型已经用于处理大规模文本数据，包括文档分类、情感分析、机器翻译和智能客服等领域。

3、生物信息学：深度学习在生物信息学中用于分析基因组、蛋白质折叠、药物发现和疾病诊断。

4、制造业：深度学习被用于质量控制、设备维护和生产过程优化，以提高制造业的效率和质量。

5、金融领域：深度学习在金融领域中应用于风险评估、欺诈检测、股票预测和量化交易策略。

深度学习的成功得益于大量可用的数据和目前强大的计算能力，以及各种深度学习架构的不断发展和改进。在工业领域，深度学习能够自动化、优化和提高许多任务的准确性和效率，因此在实际应用中具有巨大的潜力。然而，需要谨慎处理数据隐私和伦理问题，并确保模型的可解释性和可靠性。

好了，上面是咱们对深度学习在工业界的一个全面的、基本的认识。

下面咱们就以下几个方面，来聊聊各个算法的优缺点和适用场景：

前馈神经网络

卷积神经网络

循环神经网络

长短时记忆网络

生成对抗网络

自编码器

强化学习

注意力机制

图神经网络

神经图灵机

变分自编码器

序列到序列模型

前馈神经网络

前馈神经网络（Feedforward Neural Networks, FNN）主要用于构建从输入层到输出层没有反馈（即没有循环）的神经网络。

虽然”FNN”一词通常用于描述整个网络架构。

以下算法常用于训练这类网络：

1、梯度下降（Gradient Descent）

优点：

简单易于实现。

适用于大多数优化问题。

缺点：

对于非凸函数，可能陷入局部最小值。

可能需要手动设置合适的学习率。

适用场景：

简单的分类和回归问题。

2、随机梯度下降（Stochastic Gradient Descent, SGD）

优点：

计算效率高。

在处理非凸优化问题时，有更高的机会逃离局部最小值。

缺点：

可能会震荡并且不稳定。

需要手动设置学习率和其他超参数。

适用场景：

大规模数据集和在线学习。

3、小批量梯度下降（Mini-batch Gradient Descent）

优点：

结合了批量梯度下降和随机梯度下降的优点。

更加稳定，收敛速度快。

缺点：

需要选择合适的批量大小。

适用场景：

中到大规模数据集。

4、动量（Momentum）

优点：

可以更快地收敛。

能够减少震荡。

缺点：

增加了一个超参数（动量因子）。

适用场景：

非凸优化问题。

5、AdaGrad、RMSprop、Adam等自适应学习率算法

优点：

自动调整学习率。

通常比基本的梯度下降算法更快地收敛。

缺点：

实现相对复杂。

可能需要更多的计算资源。

适用场景：

高维数据集和复杂的优化问题。

这些算法都可以用于训练前馈神经网络，以解决分类、回归、聚类等各种问题。

卷积神经网络

卷积神经网络（Convolutional Neural Networks, CNN）主要用于处理具有网格结构的数据，如图像。

CNN有多种架构和优化算法。

以下是其中一些重要的，咱们摘取出来。

基础架构：

1、LeNet-5

优点：作为最早的CNN架构之一，非常简单且易于理解。

缺点：由于其简单性，对于复杂任务可能不够强大。

适用场景：手写数字识别。

2、AlexNet

优点：相对于LeNet，有更深的网络结构和更复杂的特性。

缺点：更多的参数意味着需要更多的计算资源。

适用场景：图像分类，特别是在ImageNet数据集上。

3、VGGNet

优点：使用小的卷积核（3×3）使网络更容易训练。

缺点：虽然模型结构简单，但参数量巨大。

适用场景：图像分类和物体检测。

4、GoogLeNet/Inception

优点：通过Inception模块优化了网络结构。

缺点：Inception模块增加了网络的复杂性。

适用场景：图像分类，物体检测。

5、ResNet (Residual Networks)

优点：通过残差连接解决了深度网络训练中的消失/爆炸梯度问题。

缺点：虽然可以构建非常深的网络，但这也增加了模型的复杂性。

适用场景：图像分类，物体检测，图像生成。

优化算法：

1、SGD（随机梯度下降）

优点：简单，易于实现。

缺点：可能会在局部最小值处停滞。

适用场景：几乎所有CNN结构。

2、Adam（自适应矩估计）

优点：自适应地调整学习率，通常比SGD更快收敛。

缺点：有时可能过拟合。

适用场景：快速原型设计和复杂模型。

3、RMSprop

优点：对于非凸优化问题表现很好。

缺点：学习率仍需手动设置。

适用场景：图像识别和其他复杂视觉任务。

4、Batch Normalization

优点：使网络更快地收敛，并可能提高性能。

缺点：增加了模型的复杂性和计算成本。

适用场景：几乎所有需要快速收敛的CNN。

以上只是CNN的一小部分，但这些是最广泛使用和研究的几种。

循环神经网络

循环神经网络（Recurrent Neural Networks, RNN）是用于处理序列数据的神经网络模型。

以下是一些常见的RNN算法和架构，以及它们的优缺点和适用场景：

基础架构：

1、Vanilla RNN

优点：结构简单，易于理解和实现。

缺点：难以捕捉长距离依赖关系，容易出现梯度消失或梯度爆炸问题。

适用场景：短序列任务，如文本分类和简单的时间序列预测。

2、LSTM（长短时记忆）

优点：能有效地处理长距离依赖问题，解决了梯度消失问题。

缺点：计算复杂度高，模型参数多。

适用场景：自然语言处理（如机器翻译、语音识别）、时间序列分析等。

3、GRU（门控循环单元）

优点：比LSTM简单，参数少，训练更快。

缺点：可能无法捕获与LSTM同样复杂的模式。

适用场景：与LSTM类似，但更适用于资源有限或需要快速训练的场景。

4、Bidirectional RNN

优点：能从过去和未来信息中同时学习。

缺点：需要更多的计算资源和存储。

适用场景：自然语言处理（如命名实体识别、关系抽取）、语音识别等。

优化和变种：

1、Teacher Forcing

优点：加速训练过程，提高模型性能。

缺点：可能会导致训练和测试分布不匹配。

适用场景：序列生成任务，如机器翻译。

2、Attention Mechanism

优点：提供更高层次的序列处理能力。

缺点：增加计算复杂性。

适用场景：机器翻译、文本摘要、语音识别。

3、Seq2Seq（Sequence to Sequence）

优点：可用于各种序列到序列的转换任务。

缺点：可能需要大量数据来训练成功。

适用场景：机器翻译、聊天机器人、语音识别。

4、Dropout

优点：减轻过拟合。

缺点：可能会导致欠拟合。

适用场景：几乎所有复杂的RNN模型。

5、Batch Normalization

优点：加速训练，可能提高模型性能。

缺点：增加模型复杂性。

适用场景：复杂的RNN模型，尤其是在大数据集上。

这些架构和算法通常在不同的组合和变体中出现，以解决各种序列处理问题。

长短时记忆网络

长短时记忆网络（Long Short-Term Memory，LSTM）是一种用于处理序列数据的深度学习模型，旨在克服传统循环神经网络（RNN）的梯度消失问题。LSTM引入了三个关键门控机制，允许模型更好地捕捉长期依赖关系。以下是一些与LSTM相关的算法和扩展，以及它们的优缺点和适用场景：*

1、标准LSTM

优点：能够处理长序列，捕捉长期依赖关系，适用于大多数序列建模任务。

缺点：复杂性较高，计算代价较大。

适用场景：适用于大多数序列数据的建模，包括时间序列预测、语言建模等。

2、双向LSTM（Bidirectional LSTM）

优点：能够同时考虑过去和未来的信息，更好地捕捉上下文信息，适用于自然语言处理任务和序列标注问题。

缺点：计算代价更高。

适用场景：适用于需要全局上下文信息的任务，如机器翻译和命名实体识别。

3、多层LSTM（Multilayer LSTM）

优点：通过叠加多个LSTM层，可以学习更复杂的特征，适用于深度序列建模任务。

缺点：更复杂的模型，需要更多的计算资源。

适用场景：适用于深层次的序列建模，例如机器翻译中的编码器部分。

4、GRU（Gated Recurrent Unit）

优点：与LSTM相比，GRU模型拥有更少的门控单元，计算代价较低，适用于资源受限的环境。

缺点：可能无法捕捉一些复杂的长期依赖关系。

适用场景：适用于资源有限的环境，也可用于序列建模任务。

5、Peephole LSTM

优点：在标准LSTM中引入了额外的连接，以便更好地访问内部状态，有助于提高建模能力。

缺点：计算代价较高，需要更多的参数。

适用场景：LSTM 适用于需要更好的内部状态访问的任务，如音频处理。

6、LSTM变种（如Stacked LSTM、Attention LSTM等）

优点：这些变种进一步增强了LSTM的性能，适用于各种序列任务，包括自然语言处理、机器翻译等。

缺点：通常需要更多的计算资源。

适用场景：适用于特定任务，例如Attention LSTM在机器翻译中提供更好的对齐和翻译性能。

选择合适的LSTM变种或配置取决于任务的性质、可用的计算资源以及性能需求。

生成对抗网络

生成对抗网络（Generative Adversarial Networks，GAN）是一种深度学习模型，旨在通过博弈论中的对抗训练方式生成数据。

GAN包括两个主要组件：生成器和判别器，它们相互竞争，使生成器生成更逼真的数据。

以下是一些与GAN相关的算法和扩展，以及它们的优缺点和适用场景：

1、原始GAN

优点：简单且易于理解，能够生成高质量的数据分布。

缺点：训练不稳定，容易出现模式崩溃（mode collapse）问题，需要谨慎的超参数选择。

适用场景：图像生成、样式迁移、数据增强等。

2、Deep Convolutional GAN（DCGAN）

优点：通过使用卷积层，提高了生成器和判别器的性能和稳定性。

缺点：仍然可能出现模式崩溃问题，需要大量的训练数据。

适用场景：图像生成、图像修复、超分辨率等。

3、Conditional GAN（cGAN）

优点：使生成器能够生成与给定条件相关的数据，增强了生成的控制性。

缺点：需要有条件的数据和标签，训练数据不易获得。

适用场景：图像到图像翻译、图像修复、生成特定类别的图像等。

4、Wasserstein GAN（WGAN）

优点：引入了Wasserstein距离，提高了训练的稳定性和生成质量，解决了模式崩溃问题。

缺点：计算复杂度较高，需要谨慎的网络架构设计。

适用场景：图像生成、生成真实分布的样本。

5、CycleGAN

优点：用于无监督图像到图像转换，例如照片转化为油画风格等。

缺点：需要大量数据用于无监督训练，可能无法生成高质量的细节。

适用场景：图像到图像转换，如风格转换、领域适应等。

6、Progressive GAN

优点：通过逐渐增加生成器和判别器的复杂度，生成更高分辨率的图像。

缺点：计算复杂度较高，需要大量计算资源。

适用场景：高分辨率图像生成、超分辨率、图像合成等。

7、Self-Attention GAN（SAGAN）

优点：引入自注意机制，改进了生成器对长距离依赖关系的建模，生成更高质量的图像。

缺点：计算复杂度较高，需要更多的参数。

适用场景：高质量图像生成、自然场景生成等。

选择合适的GAN变种或配置取决于任务的性质、可用的数据和计算资源，以及生成质量的要求。

GAN已广泛应用于图像生成、图像编辑、图像修复、风格迁移、文本到图像生成等各种应用领域。

八、程序员最趁手的SVM算法

线性支持向量机

非线性支持向量机

多类别支持向量机

核函数支持向量机

稀疏支持向量机

核贝叶斯支持向量机

不平衡类别支持向量机

先来啰嗦几点关于 SVM 的优势和劣势！

优势：

1、适用性广泛：SVM支持向量机在解决分类和回归问题上表现出色，可应用于各种数据类型和领域，例如文本分类、图像识别和生物信息学等。

2、鲁棒性强：SVM支持向量机对于训练数据中的噪声和异常点具有一定的鲁棒性，可以有效地处理输入数据中的噪声。

3、可避免陷入局部最优解：由于SVM支持向量机使用了结构风险最小化原则，它能够更好地避免陷入局部最优解，并且具有较低的泛化误差。

4、高维空间有效：SVM支持向量机通过核技巧将低维空间的非线性问题映射到高维空间，在高维空间中进行线性划分，从而有效地解决了复杂的非线性问题。

5、可控制的过拟合：SVM支持向量机通过调整正则化参数和松弛变量来控制模型的复杂度，从而可以有效地避免过拟合问题。

劣势：

1、计算复杂度高：SVM支持向量机在大规模数据集上的训练时间较长，特别是对于非线性问题和核函数的使用。

2、参数选择敏感：SVM支持向量机中的参数调优过程通常需要进行交叉验证，对于不同的问题和数据集，选择合适的参数可能会比较困难。

3、对缺失数据敏感：SVM支持向量机对于含有大量缺失数据的情况可能表现不佳，需要在预处理阶段进行适当的处理。

4、适用于二分类问题：原始的SVM支持向量机算法只能解决二分类问题，对于多类别问题需要进行扩展或使用其他方法。

尽管SVM支持向量机存在一些劣势，但其优势使得它成为了数据分析和机器学习领域中一个重要的算法之一。

在实际工作中，我们可以根据具体问题的特点和需求来选择合适的分类算法。

大家伙如果觉得还不错！可以点赞、转发安排起来，让更多的朋友看到

1线性支持向量机

线性支持向量机是一种用于解决分类问题的机器学习算法。

它的目标是找到一个能够在数据中画出一条直线（或者高维空间中的超平面），将不同类别的数据点分隔开，并且最大化两侧最靠近这条线的数据点之间的距离。

这两侧最靠近线的数据点被称为支持向量。

线性SVM在以下情况下非常有用：

二分类问题，即将数据分为两个类别。

当数据可以被线性分割时，即存在一条直线可以很好地将两个类别分开。

当需要一个高度可解释的模型，因为SVM的决策边界是直线或超平面，非常容易可视化和解释。

线性SVM的决策函数可以表示为：

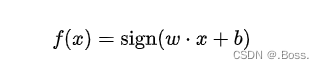
我们创建一个简单的线性SVM模型，大家可以直接运行起来：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn import svm

# 生成一些随机数据
X, y = datasets.make_classification(n_samples=100, n_features=2, n_classes=2, n_clusters_per_class=1, n_redundant=0)

# 创建SVM模型
clf = svm.SVC(kernel='linear')
clf.fit(X, y)

# 绘制数据点
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired)

# 绘制决策边界
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()

# 创建网格来评估模型
xx, yy = np.meshgrid(np.linspace(xlim[0], xlim[1], 50), np.linspace(ylim[0], ylim[1], 50))
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

# 绘制决策边界和间隔
plt.contour(xx, yy, Z, colors='k', levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--'])
plt.show()

2非线性支持向量机

非线性支持向量机的神奇之处在于，它可以帮助我们把不同形状的数据分开，像拼图一样。

有时，我们不能仅仅用一条直线分开这些数据，所以我们需要一些特殊的技巧，这就是非线性SVM的用武之地。

非线性SVM在很多情况下都非常有用，比如：

当数据不是线性分布的，也就是说，不能只用一条直线把它们分开。

当我们需要解决更复杂的问题，如图像识别或自然语言处理，这些问题通常不适合线性方法。

当我们希望用一种更复杂的方式来分隔数据，以获取更好的结果。

另外，非线性SVM的数学公式比较复杂，但我们可以简化为：它是一种方法，可以将数据映射到一个不同的空间，然后在那个空间中使用线性SVM。这个映射是通过一个叫做核函数来完成的。这个核函数通常表示为K(x,x’)，它将原始数据x和x'映射到一个新的空间。

下面是一个使用非线性SVM的Python案例，以帮助理解。

我们将使用支持向量机库svm中的SVC类，并使用径向基函数（RBF）核。

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn import svm

# 创建一些具有非线性特征的数据
X, y = datasets.make_circles(n_samples=100, factor=0.5, noise=0.1)

# 创建非线性SVM模型
clf = svm.SVC(kernel='rbf')
clf.fit(X, y)

# 绘制数据点
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired)

# 绘制决策边界
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()

# 创建网格来评估模型
xx, yy = np.meshgrid(np.linspace(xlim[0], xlim[1], 50), np.linspace(ylim[0], ylim[1], 50))
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

# 绘制决策边界和间隔
plt.contourf(xx, yy, Z, cmap=plt.cm.coolwarm, alpha=0.8)
plt.show()

3多类别支持向量机

多类别支持向量机可以应用于许多实际问题中。

比如，当我们有很多动物的照片，我们想知道每个动物的种类；或者当我们有很多水果的特征数据，我们想根据这些特征将水果分类。

我们可以用一些数学公式来描述多类别支持向量机。假设我们有n个数据点，每个数据点有两个特征，分别用x和y表示。我们还有k个类别，用1到k的数字表示。

多类别支持向量机的目标是找到一条线（或曲线），可以将不同类别的点分开。我们可以使用以下公式表示多类别支持向量机的决策规则：

from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
import matplotlib.pyplot as plt

# 加载数据集（这里使用鸢尾花数据集作为示例）
iris = datasets.load_iris()
X = iris.data[:, :2]  # 只选取前两个特征
y = iris.target

# 将数据集拆分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 创建多类别支持向量机模型，选择线性核函数
svm = SVC(kernel='linear')
svm.fit(X_train, y_train)

# 预测测试集中的类别
y_pred = svm.predict(X_test)

# 绘制决策边界和样本点
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Set1)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')

# 绘制支持向量
support_vectors = svm.support_vectors_
plt.scatter(support_vectors[:, 0], support_vectors[:, 1], s=100, facecolors='none', edgecolors='k')

# 绘制特殊点
special_points = [[5.9, 3.0], [6.2, 2.8]]
plt.scatter([point[0] for point in special_points], [point[1] for point in special_points], color='red', marker='x')

# 绘制决策边界
xlim = plt.gca().get_xlim()
ylim = plt.gca().get_ylim()
xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = svm.decision_function(xy).reshape(XX.shape)
plt.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--'])

plt.show()

4核函数支持向量机

核函数支持向量机使用场景很多，比如在图像识别、文本分类和生物信息学等领域都有应用。

核函数支持向量机的公式表达如下：

给定一个训练集 ，其中  是输入特征向量， 是对应的类别标签。核函数支持向量机的目标是找到一个超平面，将不同类别的样本分隔开来

咱们再来举一个例子：

from sklearn import svm
import matplotlib.pyplot as plt
import numpy as np

# 生成样本数据
X = np.array([[1, 2], [3, 4], [5, 6], [7, 8]])
y = np.array([0, 0, 1, 1])

# 创建核函数支持向量机模型
model = svm.SVC(kernel='rbf')

# 拟合数据
model.fit(X, y)

# 绘制决策边界
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='viridis')
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()

# 创建网格来评估模型
xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = model.decision_function(xy).reshape(XX.shape)

# 绘制决策边界和支持向量
ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5,
           linestyles=['--', '-', '--'])
ax.scatter(model.support_vectors_[:, 0], model.support_vectors_[:, 1],
           s=100, facecolors='none', edgecolors='k')

plt.show()

上述代码首先使用样本数据训练一个核函数支持向量机模型，然后通过绘制决策边界和支持向量的方式可视化分类结果。决策边界是用实线表示的，支持向量是用空心圆点表示的。

5稀疏支持向量机

当我们使用稀疏支持向量机来解决一个分类问题时，我们希望找到一个超平面，能够将不同类别的数据点有效地分开。

稀疏支持向量机通常用于处理大规模数据集或高维特征的分类问题。例如，在医学图像识别中，当需要处理数百万个像素的图像数据时，稀疏支持向量机可以高效地分类；在自然语言处理中，当需要处理大量文本特征时，该算法也能发挥作用。

给定训练数据集 ，其中  是输入特征向量， 是对应的类别标签。

稀疏支持向量机的目标是找到一个超平面，使得尽可能多的训练数据点离该超平面的距离最大化。

举一个关于稀疏支持向量机的例子，大家只要安装了相应的包即可直接运行起来：

from sklearn import svm
import matplotlib.pyplot as plt
import numpy as np

# 生成样本数据
X = np.array([[1, 2], [3, 4], [5, 6], [7, 8]])
y = np.array([0, 0, 1, 1])

# 创建稀疏支持向量机模型
model = svm.SVC(kernel='linear')

# 拟合数据
model.fit(X, y)

# 绘制数据点
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='viridis')

# 绘制超平面
w = model.coef_[0]
b = model.intercept_[0]
x_min, x_max = plt.xlim()
y_min, y_max = plt.ylim()
xx = np.linspace(x_min, x_max)
yy = -(w[0] * xx + b) / w[1]
plt.plot(xx, yy, 'k-')

# 绘制支持向量
support_vectors = model.support_vectors_
plt.scatter(support_vectors[:, 0], support_vectors[:, 1],
            s=200, facecolors='none', edgecolors='k')

plt.show()

上述代码使用给定的样本数据训练一个稀疏支持向量机模型，并绘制数据点、超平面以及支持向量。

超平面由w和b参数定义，支持向量表示离超平面最近的数据点。

九、Matplotlib总结，任何项目都用得到

如果同一个项目，你的用了matplotlib 不仅有基本图形、定制化图形、多个坐标轴、3D绘图，还有动态交互绘图、绘制地图、绘制统计图表，甚至还有地图分布！那么谁的更吸引人呢？收藏备用，一定用的上！

Matplotlib是一个功能强大且广泛使用的数据可视化工具，特别适用于科学计算、数据分析和数据科学领域。

下面是关于 Matplotlib 的一些主要特点和组成部分的介绍：

1、图表类型：包括折线图、散点图、柱状图、饼图、等高线图、热图、直方图等。这使得使用者可以根据不同的数据和需求创建不同类型的可视化图表。

2、简单易用：Matplotlib 设计简单，容易上手。用户可以使用它的基础功能来创建简单的图表，同时也可以通过自定义配置和调整来创建高度定制化的图表。

3、面向对象的接口：Matplotlib 提供了一个面向对象的接口，允许用户以程序化的方式创建和修改图表。这种接口的优点是可以更灵活地控制图表的各个组成部分，如轴、标签、标题等。

4、多种输出格式：Matplotlib 支持将图表以多种格式保存，包括图像文件（如PNG、JPEG、SVG等）和交互式图表，使用户能够在不同的场景中分享和使用图表。

5、扩展性：Matplotlib 可以通过各种插件和扩展库进行扩展，以满足更高级的数据可视化需求。例如，Seaborn、Pandas 和 Plotly 都是建立在 Matplotlib 基础之上的库。

6、跨平台：Matplotlib 可以在多个操作系统上运行，包括 Windows、Linux 和 macOS，因此适用于各种开发环境。

本文将从绘制基本图形、定制化图形、多个坐标轴、3D绘图、动态交互绘图、绘制地图、绘制统计图表等等方面进行全方位介绍！

大家伙如果觉得还不错！可以点赞、收藏支持一下谢谢。

目录

1、绘制基本图形

2、定制化图形

3、支持多个坐标轴

4、3D绘图

5、动态交互绘图

6、绘制地图

7、绘制统计图表

最后

---

1、绘制基本图形

Matplotlib 可以绘制许多基本的图形，包括但不限于以下类型：

折线图（Line Plot）：用于显示数据随时间或其他连续变量的变化趋势。

散点图（Scatter Plot）：用于展示两个变量之间的关系，通常用于观察数据的分布和离群点。

柱状图（Bar Plot）：用于比较不同类别的数据，通常用于展示离散数据的分布。

饼图（Pie Chart）：用于表示数据的相对部分，展示各部分在整体中的比例。

直方图（Histogram）：用于展示数据的分布情况，特别适用于连续数据的分布分析。

箱线图（Box Plot）：用于显示数据的统计信息，包括中位数、上下四分位数和离群值等。

等高线图（Contour Plot）：用于可视化二维数据集中的等高线，通常在地理信息系统和物理学领域中使用。

热图（Heatmap）：用于显示数据的热度或相关性，通常以颜色编码方式表示数值。

下面演示一个直方图：

import numpy as np
import matplotlib.pyplot as plt

# 生成大数据量（随机生成）
data = np.random.randn(100000)

# 配置图形和颜色
plt.figure(figsize=(10, 6))  # 设置图形大小
plt.hist(data, bins=50, color='skyblue', edgecolor='black')  # 绘制直方图
plt.title('Histogram of Large Data')  # 设置标题
plt.xlabel('Value')  # 设置X轴标签
plt.ylabel('Frequency')  # 设置Y轴标签

# 显示图形
plt.show()

上述代码创建了一个直方图，包括以下特点：

使用 np.random.randn 生成了大量随机数据，模拟了大数据量。

通过 plt.figure 来设置图形的大小。

使用 plt.hist 创建直方图，配置了颜色为天蓝色 ('skyblue')，边缘颜色为黑色 ('black')，并设置了数据分组的数量 (bins)。

添加了标题、X轴标签和Y轴标签。

最后，通过 plt.show() 显示图形。

实际情况中，可以根据需要自定义图形的颜色、样式、标签等属性，以满足具体的可视化需求。

2、定制化图形

Matplotlib 提供了丰富的选项来自定义图形，包括颜色、线型、标签、标题和图例等。

下面演示如何使用 Matplotlib 定制化一个图形，分别单独调整这些属性。

我们绘制一个简单的折线图，并对其进行定制化：

import numpy as np
import matplotlib.pyplot as plt

# 创建数据
x = np.linspace(0, 2 * np.pi, 100)
y1 = np.sin(x)
y2 = np.cos(x)

# 创建图形
plt.figure(figsize=(10, 6))  # 设置图形大小

# 绘制两个曲线，分别定制化颜色、线型、标签
plt.plot(x, y1, color='blue', linestyle='-', linewidth=2, label='Sine Wave')
plt.plot(x, y2, color='red', linestyle='--', linewidth=2, label='Cosine Wave')

# 设置标题和坐标轴标签
plt.title('Customized Sine and Cosine Waves')
plt.xlabel('X-axis')
plt.ylabel('Y-axis')

# 添加图例，并设置位置、标题
plt.legend(loc='upper right', title='Legend')
plt.grid(True)  # 添加网格线

# 注释一些特殊点
plt.annotate('Peak', xy=(np.pi / 2, 1), xytext=(np.pi / 2, 1.5),
             arrowprops=dict(facecolor='black', shrink=0.05),
             )
plt.annotate('Trough', xy=(3 * np.pi / 2, -1), xytext=(3 * np.pi / 2, -1.5),
             arrowprops=dict(facecolor='black', shrink=0.05),
             )

# 设置坐标轴范围
plt.xlim(0, 2 * np.pi)
plt.ylim(-2, 2)

# 显示图形
plt.show()

上述代码创建了一个折线图：

color='blue'：设置折线的颜色为蓝色。

linestyle='--'：设置折线的线型为虚线。

linewidth=2：设置折线的宽度为2。

label='Sine Wave'：设置图例的标签为”Sine Wave”。

plt.title、plt.xlabel、plt.ylabel 分别用于设置标题、X轴标签和Y轴标签。

plt.legend(loc='upper right')：添加图例并指定位置为右上角。

通过类似的方式，可以进一步定制化其他类型的图形，例如散点图、柱状图等，并根据需求调整颜色、线型、标签、标题和图例等属性。

Matplotlib 提供了丰富的选项，完全可以满足各种数据可视化需求。

3、支持多个坐标轴

Matplotlib是一个强大的Python数据可视化库，允许在同一个图中使用多个坐标轴，创建更加灵活和丰富的图形。

下面的示例中，创建一个包含主轴和次轴的复杂图形，展示Matplotlib中多个坐标轴的使用方法。

这个示例图形将包括一条正弦曲线和一条余弦曲线，它们使用不同的刻度和坐标轴。

import matplotlib.pyplot as plt
import numpy as np

# 创建新的图形和主要坐标轴
fig, ax1 = plt.subplots()

# 设置主要坐标轴的标签和标题
ax1.set_xlabel('X-axis')
ax1.set_ylabel('Primary Axis - Sine Curve', color='tab:blue')

# 生成X轴数据
x = np.linspace(0, 10, 100)
# 生成正弦曲线的Y轴数据
y1 = np.sin(x)

# 在主要坐标轴上绘制正弦曲线
ax1.plot(x, y1, color='tab:blue')

# 创建共享相同X轴的次要坐标轴
ax2 = ax1.twinx()

# 设置次要坐标轴的标签
ax2.set_ylabel('Secondary Axis - Cosine Curve', color='tab:red')

# 生成余弦曲线的Y轴数据
y2 = np.cos(x)

# 在次要坐标轴上绘制余弦曲线
ax2.plot(x, y2, color='tab:red')

# 添加图例
ax1.legend(['Sine Curve'], loc='upper left')
ax2.legend(['Cosine Curve'], loc='upper right')

# 添加网格线
ax1.grid()

plt.title('Primary and Secondary Axis Example')
plt.show()

在这个示例中，首先创建了一个包含主轴（ax1）的Figure，并绘制了正弦曲线。

然后，我们创建了一个共享X轴的次轴（ax2），并在次轴上绘制了余弦曲线。

还对每个轴设置了标题、标签、颜色，并添加了图例和网格线，以增强图形的可读性。

这个示例展示了使用多个坐标轴创建的图形，实际使用中可以根据自己的需求进一步自定义和扩展图形。

4、3D绘图

Matplotlib是一个用于数据可视化的Python库，它支持绘制各种类型的图形，包括三维图形。

在Matplotlib中，比如可以使用mpl_toolkits.mplot3d模块来创建和绘制三维图形。

下面绘制一个简单的三维表面图，包括主轴和次轴，大家可以简单看下，明白其中的原理。

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np

# 创建一个三维图形的figure
fig = plt.figure()

# 创建一个三维坐标轴
ax = fig.add_subplot(111, projection='3d')

# 创建数据
# 这里我们以一个二维的网格为例，生成X和Y坐标，然后使用一个函数来计算Z坐标
X = np.arange(-5, 5, 0.25)
Y = np.arange(-5, 5, 0.25)
X, Y = np.meshgrid(X, Y)
Z = np.sin(np.sqrt(X**2 + Y**2))

# 绘制表面图
surf = ax.plot_surface(X, Y, Z, cmap='viridis')

# 添加颜色条
fig.colorbar(surf)

# 设置坐标轴标签
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')

# 显示图形
plt.show()

上述代码中，首先创建了一个figure，然后在该figure上创建了一个三维坐标轴ax。

接下来，生成了X、Y坐标的网格数据，并使用一个简单的函数计算Z坐标。

然后，使用plot_surface方法绘制了表面图，并使用cmap参数设置了颜色映射。

最后，我们添加了颜色条和坐标轴标签，并显示了图形。

Matplotlib提供了丰富的功能和选项来创建各种类型的三维图形，以展示更复杂的数据关系。

5、动态交互绘图

Matplotlib还可以用于创建静态和动态交互图形。

这个知识点中，简要介绍如何使用Matplotlib创建一个允许用户进行交互操作的动态图形。

接下来，我们将使用Matplotlib的FuncAnimation类来创建一个动态图形，同时也会使用IPython的display函数来在Jupyter Notebook中实时显示动画。

这里绘制一个简单的正弦波，并且可以通过滑块来控制波的频率。

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from IPython.display import display, clear_output

# 创建一个空白图形
fig, ax = plt.subplots()

# 定义正弦波的参数
x = np.linspace(0, 2 * np.pi, 1000)
freq = 1.0  # 初始频率

# 初始绘制正弦波
line, = ax.plot(x, np.sin(freq * x))

# 添加滑块用于控制频率
from ipywidgets import interactive
import ipywidgets as widgets

def update(freq=1.0):
    # 更新正弦波的频率
    line.set_ydata(np.sin(freq * x))
    ax.set_ylim(-1.5, 1.5)
    ax.set_title(f'Sine Wave (Frequency: {freq:.2f} Hz)')
    display(fig)

# 创建交互式滑块
slider = widgets.FloatSlider(value=1.0, min=0.1, max=5.0, step=0.1, description='Frequency')
interactive_plot = interactive(update, freq=slider)

# 显示动态图形
display(interactive_plot)

# 如果在Jupyter Notebook中使用，你会看到一个滑块，通过滑块可以调整正弦波的频率。

可以通过滑块来调整波的频率。

在Jupyter Notebook中执行这段代码，然后通过滑动滑块来与图形进行交互。

FuncAnimation类用于创建动画效果，interactive函数用于创建交互式滑块。

可以使用Matplotlib创建各种类型的交互式图形，以满足具体的需求。

6、绘制地图

Matplotlib 还可以绘制地图和等高线图。

如果要绘制一个复杂一些的等高线图，需要使用一些额外的库，比如 NumPy 和 Cartopy（用于地图投影）。

下面演示如何使用 Matplotlib、NumPy 和 Cartopy 来绘制一个地理高程的等高线图。

除了Matplotlib、NumPy，记得需要把 Cartopy 安装好。

pip install cartopy

然后，使用以下示例代码来绘制等高线图：

import numpy as np
import matplotlib.pyplot as plt
import cartopy.crs as ccrs
import cartopy.feature as cfeature

# 创建一个地图投影
projection = ccrs.PlateCarree()

# 创建一个 Matplotlib 图形窗口
fig, ax = plt.subplots(subplot_kw={'projection': projection}, figsize=(10, 8))

# 创建一些示例数据（高程数据）
# 这里使用 NumPy 创建一个 2D 数组，表示高程值
# 你可以根据你的数据替换这些值
lats = np.linspace(-90, 90, 360)
lons = np.linspace(-180, 180, 720)
lons, lats = np.meshgrid(lons, lats)
elevation_data = np.sin(np.radians(lats)) * np.cos(np.radians(lons)) * 1000

# 添加等高线图
contour = plt.contourf(lons, lats, elevation_data, levels=20, cmap='terrain')

# 添加海岸线和国界线
ax.add_feature(cfeature.COASTLINE)
ax.add_feature(cfeature.BORDERS, linestyle=':')

# 添加颜色条
cbar = plt.colorbar(contour, ax=ax, shrink=0.8, orientation='horizontal')
cbar.set_label('Elevation (m)')

# 设置地图范围（中国）
ax.set_extent([73, 135, 8, 53], crs=projection)

# 添加标题
plt.title('Elevation Contour Map')

# 显示图形
plt.show()

上述代码创建了一个基本的等高线图，使用了 Cartopy 进行地图投影和地图要素的添加，以及 Matplotlib 进行绘图和图形设置。

如果显示范围是世界地图的话，修改这里的设置即可！

# 设置地图范围
ax.set_extent([-180, 180, -90, 90], crs=projection)

7、绘制统计图表

Matplotlib 也可以绘制统计图表，包括箱线图（Box Plot），也称为盒图或箱型图。

箱线图是一种可视化数据分布的方式，它显示了数据的中位数、四分位数、异常值等信息。

下面是一个使用Matplotlib绘制箱线图的示例：

import matplotlib.pyplot as plt
import numpy as np

# 创建示例数据
data = [np.random.normal(0, std, 100) for std in range(1, 5)]

# 创建箱线图
plt.figure(figsize=(8, 6))
plt.boxplot(data, vert=True, patch_artist=True, labels=['A', 'B', 'C', 'D'], notch=True)

# 添加标题和标签
plt.title('Box Plot Example')
plt.xlabel('Groups')
plt.ylabel('Values')

# 自定义箱线的填充颜色
box_colors = ['lightblue', 'lightgreen', 'lightpink', 'lightyellow']
for box, color in zip(plt.boxplot(data, vert=True, patch_artist=True)['boxes'], box_colors):
    box.set_facecolor(color)

# 添加网格线
plt.grid(True, linestyle='--', alpha=0.7)

# 显示图形
plt.show()

首先创建了一些示例数据，其中包括四组具有不同标准差的正态分布数据。

然后，我们使用plt.boxplot函数绘制箱线图。参数解释如下：

data：包含数据的列表，每个列表对应一个箱线图。

vert：设置为True以垂直绘制箱线图。

patch_artist：设置为True以允许自定义箱线图的样式。

labels：用于指定每个箱线图的标签。

notch：设置为True以在箱线图的中位数处添加缺口。

还自定义了箱线的填充颜色，并添加了标题、标签和网格线。

这个示例中的箱线图是一个简单示例，你可以根据实际情况对其进行更复杂的定制。

总的来说，Matplotlib 是一个强大而灵活的 Python 数据可视化工具，可用于创建各种类型的图表，帮助用户更好地理解和呈现数据。如果你需要在数据分析和可视化中使用 Python，Matplotlib 是一个不可或缺的工具之一。

十、机器学习7大方面，30个硬核数据集

在刚刚开始学习算法的时候，大家有没有过这种感觉，最最重要的那必须是算法本身！

其实在一定程度上忽略了数据的重要性。

而事实上一定是，质量高的数据集可能是最重要的！

数据集在机器学习算法项目中具有非常关键的重要性，数据集的大小、质量的高低对整个项目的成功和模型性能的影响是至关重要的。

总结了6 方面：

1、决定模型性能：一个好的数据集可以让模型更准确，而低质量或小规模的数据集可能导致模型表现不佳。

2、特征选择和工程： 合适的特征选择和工程能够提高模型的泛化能力。

3、模型训练和评估： 好的数据集能够确保模型在不同数据上的泛化能力。

4、过拟合和欠拟合： 数据集的大小和质量可以影响模型的过拟合和欠拟合情况。较小的数据集更容易过拟合，而低质量数据可能导致欠拟合。

5、数据偏差： 数据集的不平衡分布或偏斜可能导致模型的偏差。

6、数据清洗和预处理： 数据集需要进行清洗和预处理，以处理缺失数据、异常值和重复数据。这是确保数据质量的重要步骤。

数据集是机器学习项目的基石。选择适当的数据集、数据清洗、特征工程和数据预处理等步骤都需要谨慎处理，以确保模型能够在实际应用中取得良好的效果。数据集的质量和数量都是决定模型成功的关键要素。

下面是涉及回归、分类、图像分类、文本情感分析、自然语言处理、自动驾驶和金融领域的30个常见机器学习数据集，以及每个数据集的介绍、获取链接和可能涉及到的算法。

回归问题

1、Boston Housing 数据集

介绍： 包含波士顿地区的住房价格数据。

获取方式： Scikit-learn内置数据集。

from sklearn.datasets import load_boston

boston = load_boston()

# 特征矩阵
X = boston.data

# 目标向量（房价）
y = boston.target

涉及算法： 线性回归、岭回归、随机森林。

2、California Housing 数据集

介绍： 包含加利福尼亚州地区的住房价格数据。

获取方式： Scikit-learn内置数据集。

from sklearn.datasets import fetch_california_housing

# 使用fetch_california_housing函数加载数据集
california_housing = fetch_california_housing()

# 特征矩阵
X = california_housing.data

# 目标向量（房屋价值的中位数）
y = california_housing.target

涉及算法： 线性回归、决策树、支持向量机。

3、Diabetes 数据集

介绍： 包含糖尿病患者的医疗数据，用于预测糖尿病进展。

获取方式： Scikit-learn内置数据集。

from sklearn.datasets import load_diabetes

# 使用load_diabetes函数加载数据集
diabetes = load_diabetes()

# 特征矩阵
X = diabetes.data

# 目标向量（糖尿病进展指数）
y = diabetes.target

涉及算法： 线性回归、支持向量机、决策树。

4、Wine Quality 数据集

介绍： 包含红葡萄酒和白葡萄酒的化学分析数据，用于预测质量评分。

获取链接：https://archive.ics.uci.edu/ml/datasets/wine+quality

涉及算法： 线性回归、决策树、随机森林。

5、Airlines 数据集

介绍： 包含航班延误和性能数据。

获取链接：https://www.transtats.bts.gov/DL_SelectFields.asp

涉及算法： 线性回归、时间序列分析。

6、Energy Efficiency 数据集

介绍： 包含建筑能源效率的数据。

获取链接：https://archive.ics.uci.edu/ml/datasets/Energy+efficiency

涉及算法： 线性回归、岭回归、支持向量机。

7、Bike Sharing 数据集

介绍： 包含自行车租赁数据，涉及天气和日期信息。

获取链接： https://archive.ics.uci.edu/ml/datasets/Bike+Sharing+Dataset

涉及算法： 线性回归、决策树、随机森林。

8、Life Expectancy 数据集

介绍： 包含各国生活预期和卫生数据。

获取链接： https://www.kaggle.com/kumarajarshi/life-expectancy-who

涉及算法： 线性回归、决策树、随机森林。

9、NYC Yellow Taxi 数据集

介绍： 包含纽约市黄色出租车的行程数据。

获取链接： https://www1.nyc.gov/site/tlc/about/tlc-trip-record-data.page

涉及算法： 时间序列分析、线性回归、岭回归。

10、Forest Fires 数据集

介绍： 包含葡萄牙森林火灾数据，用于预测火灾规模。

获取链接：https://archive.ics.uci.edu/ml/datasets/Forest+Fires

涉及算法：线性回归、决策树、随机森林。

分类问题

11、Iris 数据集

介绍： 包含三种不同种类的鸢尾花的测量数据。

获取方式： Scikit-learn内置数据集。

from sklearn.datasets import load_iris

# 使用load_iris函数加载数据集
iris = load_iris()

# 特征矩阵
X = iris.data

# 目标向量（鸢尾花的类别）
y = iris.target

涉及算法： 决策树、支持向量机、k-最近邻算法。

12、Breast Cancer 数据集

介绍： 用于分类乳腺肿瘤是否为恶性或良性。

获取链接：https://archive.ics.uci.edu/ml/datasets/Breast+Cancer+Wisconsin+%28Diagnostic%29

涉及算法： 逻辑回归、支持向量机、决策树。

13、Wine 数据集

介绍： 包含三个不同种类的葡萄酒的化学分析数据。

获取链接：https://archive.ics.uci.edu/ml/datasets/wine

涉及算法： 主成分分析（PCA）、支持向量机、k-最近邻算法。

图像分类

14、MNIST 数据集

介绍： 包含手写数字图像数据集。

获取链接：http://yann.lecun.com/exdb/mnist/

涉及算法： 卷积神经网络（CNN）、深度学习。

15、CIFAR-10 数据集

介绍： 包含10个不同类别的小图像数据集。

获取链接： https://www.cs.toronto.edu/~kriz/cifar.html

涉及算法： 卷积神经网络（CNN）、深度学习。

16、ImageNet 数据集

介绍： 包含数百万张图像，涵盖数千个不同类别。

获取链接： http://www.image-net.org/

涉及算法： 卷积神经网络（CNN）、迁移学习。

17、Fashion MNIST 数据集

介绍： 与MNIST类似，但包含了10个不同种类的时尚物品的图像。

获取链接：https://github.com/zalandoresearch/fashion-mnist

涉及算法：卷积神经网络（CNN）、多层感知机（MLP）。

18、Dogs vs、Cats 数据集

介绍： 包含狗和猫的图像，用于图像分类任务。

获取链接：https://www.kaggle.com/c/dogs-vs-cats

涉及算法：卷积神经网络（CNN）、迁移学习。

文本情感分析

19、IMDb 电影评分数据集

介绍： 包含电影的评分和评论数据。

获取链接：https://www.imdb.com/interfaces/

涉及算法： 自然语言处理模型、推荐系统、情感分析。

20、Yelp 数据集

介绍： 包含用户对商家的评论和评分数据。

获取链接：https://www.yelp.com/dataset

涉及算法： 自然语言处理模型、推荐系统、卷积神经网络。

21、Amazon 评论数据集

介绍： 包含亚马逊产品的评论和评分数据。

获取链接：https://registry.opendata.aws/amazon-reviews/

涉及算法： 自然语言处理模型、推荐系统、情感分析。

22、Spam SMS 数据集

介绍： 包含垃圾短信和非垃圾短信的文本数据。

获取链接：https://www.kaggle.com/datasets/uciml/sms-spam-collection-dataset

涉及算法： 自然语言处理模型、朴素贝叶斯、支持向量机。

23、Twitter 情感分析数据集

介绍： 包含推文的情感分析数据。

获取链接：http://help.sentiment140.com/for-students

涉及算法： 自然语言处理模型、情感分析。

自然语言处理

24、Penn Treebank 数据集

介绍： 包含句子和标签，用于语法分析和自然语言处理任务。

获取链接：https://catalog.ldc.upenn.edu/LDC99T42

涉及算法： 循环神经网络（RNN）、长短时记忆网络（LSTM）。

25、Gutenberg 电子书数据集

介绍： 包含大量文学作品的文本数据，可用于文本分析和自然语言处理。

获取链接：http://www.gutenberg.org/

涉及算法： 文本分析、主题建模、情感分析。

26、20 Newsgroups 数据集

介绍： 包含新闻组文章的文本数据，用于文本分类和主题建模。

获取方式： Scikit-learn内置数据集。

from sklearn.datasets import fetch_20newsgroups

# 使用fetch_20newsgroups函数加载数据集
newsgroups = fetch_20newsgroups(subset='all', remove=('headers', 'footers', 'quotes'))

# 文本数据
X = newsgroups.data

# 目标向量（新闻组类别）
y = newsgroups.target

涉及算法： 朴素贝叶斯、支持向量机、自然语言处理模型。

自动驾驶

27、Udacity Self-Driving Car 数据集

介绍： 包含来自Udacity自动驾驶汽车的传感器数据。

获取链接：https://github.com/udacity/self-driving-car

涉及算法： 深度学习、卷积神经网络、循环神经网络。

28、KITTI Vision Benchmark Suite 数据集

介绍： 包含来自自动驾驶测试车的图像、点云和GPS数据。

获取链接：http://www.cvlibs.net/datasets/kitti/

涉及算法： 计算机视觉、深度学习、激光雷达处理。

金融类

29、LendingClub 数据集

介绍： 包含借贷交易的数据，用于信用风险评估。

获取链接：https://www.kaggle.com/datasets/wordsforthewise/lending-club

涉及算法： 逻辑回归、随机森林、梯度提升。

30、NYC Taxi Trip 数据集

介绍： 包含纽约市出租车行程数据，用于预测乘客付费。

获取链接：https://www.kaggle.com/c/nyc-taxi-trip-duration

涉及算法： 回归分析、时间序列分析、深度学习。

最后

最后聊一聊，获取一些数据集可能需要注册或符合特定使用条件。此外，对于图像分类、文本情感分析和自然语言处理等任务，还可以使用深度学习技术，如卷积神经网络（CNN）、循环神经网络（RNN）和预训练模型（如BERT）。对于自动驾驶任务，需要结合计算机视觉和传感器数据处理。金融领域的数据集通常用于建立量化金融模型和风险分析。